题目内容
已知函数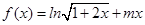 .
.
(Ⅰ)若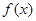 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数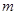 的取值范围;
的取值范围;
(Ⅱ)当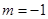 时,求函数
时,求函数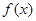 的最大值;
的最大值;
(Ⅲ)当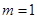 时,且
时,且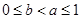 ,证明:
,证明: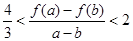 .
.
(1) 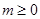 (2)
(2) 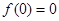
(3)根据题意,构造函数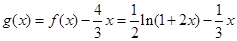 ,利用导数判定单调性的运用,然后求证明不等式。
,利用导数判定单调性的运用,然后求证明不等式。
解析试题分析:解:(Ⅰ)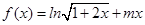 ,
, ∴
∴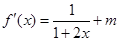
因为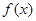 为定义域上的单调增函数,由
为定义域上的单调增函数,由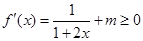 对
对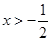 恒成立, ∴
恒成立, ∴ ,而
,而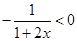 ,所以
,所以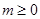
∴当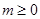 时,
时,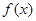 为定义域上的单调增函数
为定义域上的单调增函数
(Ⅱ)当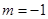 时,由
时,由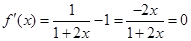 ,得
,得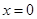
当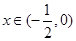 时,
时,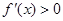 ,当
,当 时,
时,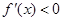
∴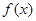 在
在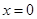 时取得最大值,∴此时函数
时取得最大值,∴此时函数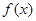 的最大值为
的最大值为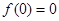
(Ⅲ) 当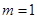 时,
时,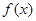 在
在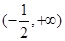 上递增
上递增
令
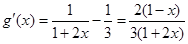 在
在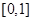 上总有
上总有 ,即
,即 在
在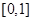 上递增
上递增
当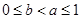 时,
时, ,
,
即
令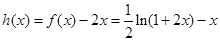 ,
,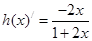 ,在
,在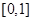 上
上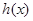 递减, ∴
递减, ∴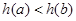 即
即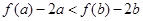 ,
, ∵
∵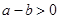 ,∴
,∴ ,综上
,综上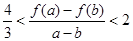 成立,其中
成立,其中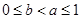 .
.
考点:函数的单调性
点评:主要是考查了函数的单调性和导数符号之间关系的运用,属于中档题。

练习册系列答案
相关题目
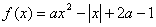 ,(
,( 为实常数)
为实常数)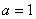 ,将
,将 写出分段函数的形式,并画出简图,指出其单调递减区间;
写出分段函数的形式,并画出简图,指出其单调递减区间;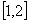 上的最小值为
上的最小值为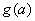 ,求
,求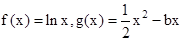 (b为常数).
(b为常数).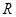 上奇函数
上奇函数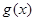 与偶函数
与偶函数 ,对任意
,对任意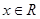 满足
满足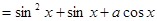 a为实数
a为实数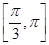 上的最值
上的最值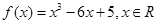
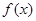 的单调区间和极值;
的单调区间和极值;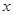 的方程
的方程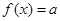 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.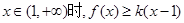 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.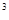 +3x
+3x +9x+a
+9x+a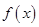 满足
满足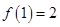 ,且当
,且当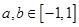 ,
,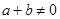 时,有
时,有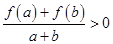 .
.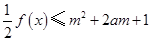 对所有
对所有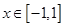 ,
,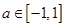 恒成立,
恒成立,
 的奇偶性
的奇偶性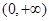 上单调递增
上单调递增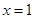 是函数
是函数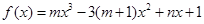 的一个极值点,其中
的一个极值点,其中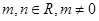
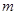 与
与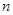 的关系式;
的关系式;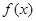 的单调区间;
的单调区间;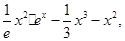
 ;试比较g(x)与
;试比较g(x)与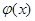 的大小。
的大小。