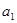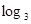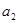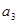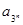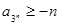题目内容
定义在[-1,1]上的奇函数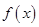 满足
满足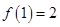 ,且当
,且当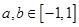 ,
,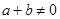 时,有
时,有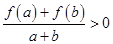 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若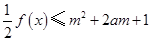 对所有
对所有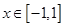 ,
,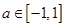 恒成立,
恒成立,
求实数m的取值范围.
(1)根据函数单调性的定义,设变量作差变形定号下结论。
(2)实数m的取值范围是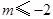 或
或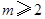 或
或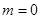 .
.
解析试题分析:解:(1)假设函数的图象上存在两个满足条件的点A,B,则它们的纵坐标相同
任取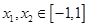 ,且
,且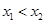 , 则
, 则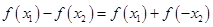
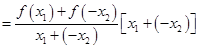 4分
4分
因为 ,
,
所以,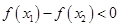
∴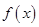 是[-1,1]上的增函数 6分
是[-1,1]上的增函数 6分
这与假设矛盾,所以假设不成立,
∴ 函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直 8分
(2)要使得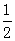
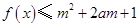 对所有
对所有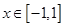 ,
,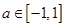 恒成立,
恒成立,
只须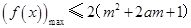 , 11分
, 11分
由(1)得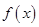 是[-1,1]上的增函数 ∴
是[-1,1]上的增函数 ∴
∴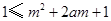 对任意的
对任意的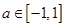 恒成立 3分
恒成立 3分
令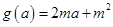 ,则只须
,则只须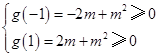 ,
,
解之得: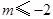 或
或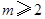 或
或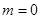 15分
15分
∴实数m的取值范围是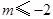 或
或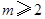 或
或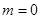 . 16分
. 16分
考点:函数的奇偶性和单调性
点评:解决的关键是利用单调性的定义证明,同事利用不等式恒成立来化简为分离参数的思想来求解最值得到参数的范围。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
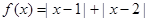
 的图象;
的图象;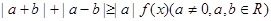 恒成立,求实数
恒成立,求实数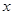 的范围.
的范围.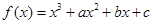 在
在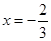 与
与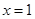 时都取得极值.
时都取得极值. 的值与函数
的值与函数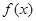 的单调区间
的单调区间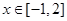 ,不等式
,不等式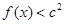 恒成立,求
恒成立,求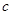 的取值范围。
的取值范围。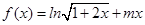 .
.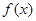 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数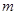 的取值范围;
的取值范围;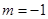 时,求函数
时,求函数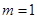 时,且
时,且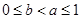 ,证明:
,证明: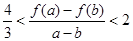 .
.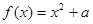 .
.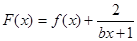 是偶函数,在定义域上
是偶函数,在定义域上 恒成立,求实数
恒成立,求实数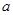 的取值范围;
的取值范围;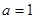 时,令
时,令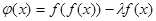 ,问是否存在实数
,问是否存在实数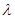 ,使
,使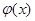 在
在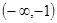 上是减函数,在
上是减函数,在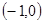 上是增函数?如果存在,求出
上是增函数?如果存在,求出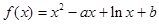
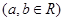 ,
,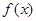 在
在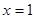 处的切线方程为
处的切线方程为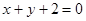 ,求实数
,求实数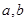 的值;
的值;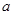 的取值范围.
的取值范围.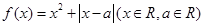 .
.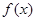 的奇偶性;
的奇偶性;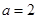 时,求
时,求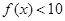 对
对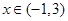 恒成立,求实数
恒成立,求实数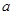 的取值范围.
的取值范围.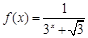 ,(1)分别求
,(1)分别求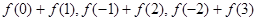 ;(2)然后归纳猜想一般性结论,并给出证明.
;(2)然后归纳猜想一般性结论,并给出证明. 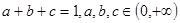 ,求证:
,求证: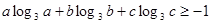 ;
;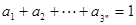 ,
,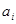 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: