题目内容
已知函数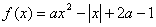 ,(
,( 为实常数)
为实常数)
(1)若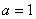 ,将
,将 写出分段函数的形式,并画出简图,指出其单调递减区间;
写出分段函数的形式,并画出简图,指出其单调递减区间;
(2)设 在区间
在区间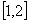 上的最小值为
上的最小值为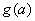 ,求
,求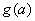 的表达式。
的表达式。
(1)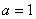 ,
,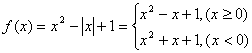
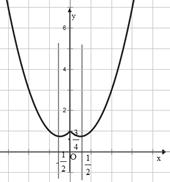
 的单调递减区间为
的单调递减区间为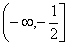 和
和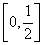 ;
;
(2)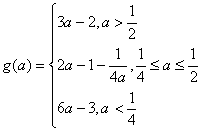 12分
12分
解析试题分析:(1)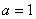 ,
,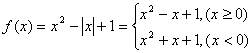 2分
2分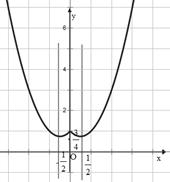
4分 的单调递减区间为
的单调递减区间为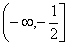 和
和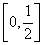 6分
6分
(2)当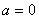 时,
时,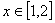 ,
,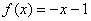 ,在
,在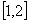 上单调递减,
上单调递减, 当
当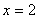 时,
时,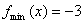 7分
7分
当 时,
时,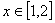 ,
,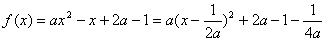
(ⅰ)当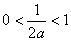 ,即
,即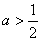 时,此时
时,此时 在
在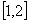 上单调递增,
上单调递增,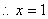 时,
时,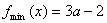
(ⅱ)当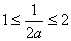 ,即
,即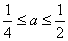 时,当
时,当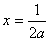 时,
时,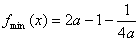
(ⅲ)当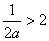 ,即
,即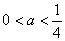 时,此时
时,此时 在
在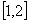 上单调递减,
上单调递减,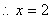 时
时 9分
9分
当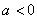 时,
时,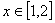 ,
,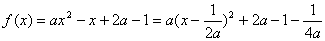 ,此时
,此时 在
在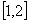 上单调递减,
上单调递减,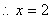 时
时 10分
10分
综上: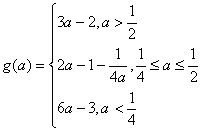 12分
12分
考点:本题主要考查分段函数的概念,绝对值的概念,二次函数的图象和性质。
点评:中档题,本题综合考查分段函数的概念,绝对值的概念,二次函数的图象和性质。从解法看,思路比较明确,但操作上易于出错。(2)涉及求闭区间上二次函数的最值问题,注意讨论对称轴与区间的相对位置,确定得到最值的不同表达式。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的奇函数f(x)在
上的奇函数f(x)在 上是减函数,若f(1-m)< f(m)
上是减函数,若f(1-m)< f(m) 的取值范围.
的取值范围. 上有意义的两个函数
上有意义的两个函数 ,如果对于任意的
,如果对于任意的 ,都有
,都有 则称
则称 给定一个区间
给定一个区间 。
。 在区间
在区间 的取值范围;
的取值范围; 在区间
在区间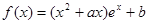 ,
,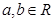 ,若函数
,若函数 在
在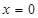 处的切线方程为
处的切线方程为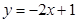 ,
,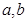 的值;
的值;
 时,求函数
时,求函数 的极值;
的极值; 时,讨论函数
时,讨论函数 及任意
及任意 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.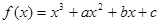 的图象过点
的图象过点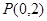 ,且点
,且点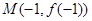 处的切线方程为在
处的切线方程为在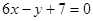 .
. 的解析式; (2)求函数
的解析式; (2)求函数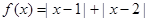
 的图象;
的图象; 恒成立,求实数
恒成立,求实数 的范围.
的范围.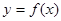 在
在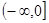 上递增,函数f(x)的一个零点为
上递增,函数f(x)的一个零点为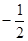 ,
,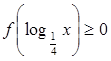 的x的取值集合.
的x的取值集合.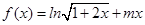 .
.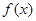 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数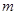 的取值范围;
的取值范围;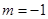 时,求函数
时,求函数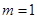 时,且
时,且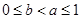 ,证明:
,证明: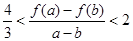 .
.