题目内容
(本小题满分12分)已知定义在实数集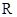 上的奇函数
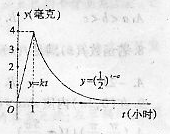
上的奇函数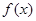 有最小正周期2,且当
有最小正周期2,且当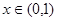 时,
时,
(Ⅰ)求函数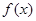 在
在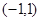 上的解析式; (Ⅱ)判断
上的解析式; (Ⅱ)判断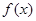 在
在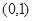 上的单调性;
上的单调性;
(Ⅲ)当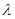 取何值时,方程
取何值时,方程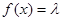 在
在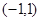 上有实数解?
上有实数解?
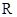 上的奇函数
上的奇函数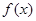 有最小正周期2,且当
有最小正周期2,且当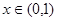 时,
时,
(Ⅰ)求函数
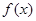 在
在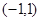 上的解析式; (Ⅱ)判断
上的解析式; (Ⅱ)判断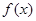 在
在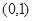 上的单调性;
上的单调性;(Ⅲ)当
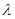 取何值时,方程
取何值时,方程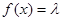 在
在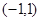 上有实数解?
上有实数解?解:(Ⅰ)∵f(x)是x∈R上的奇函数,∴f(0)="0. " ---------1分
设x∈(-1,0), 则-x∈(0,1),
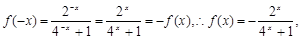 ---------2分
---------2分
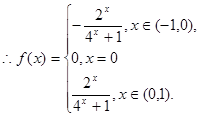 ---------3分
---------3分
(Ⅱ)设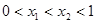 ,
,
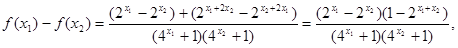 ------4分
------4分
∵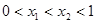 ,∴
,∴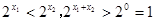 , ---------5分
, ---------5分
∴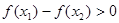
∴f(x)在(0,1)上为减函数. ---------6分
(Ⅲ)∵f(x)在(0,1)上为减函数,
∴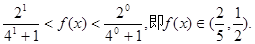 ---------7分
---------7分
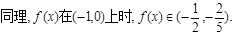 ---------8分
---------8分
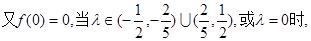
方程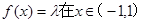 上有实数解. -----------------10分
上有实数解. -----------------10分
设x∈(-1,0), 则-x∈(0,1),
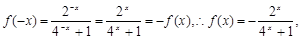 ---------2分
---------2分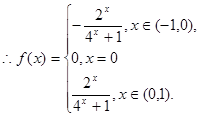 ---------3分
---------3分(Ⅱ)设
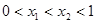 ,
,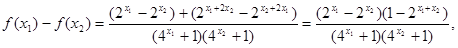 ------4分
------4分∵
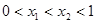 ,∴
,∴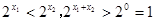 , ---------5分
, ---------5分∴
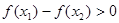
∴f(x)在(0,1)上为减函数. ---------6分
(Ⅲ)∵f(x)在(0,1)上为减函数,
∴
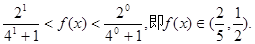 ---------7分
---------7分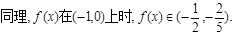 ---------8分
---------8分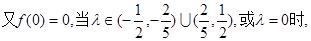
方程
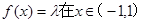 上有实数解. -----------------10分
上有实数解. -----------------10分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
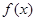 在
在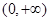 上是增函数,试问
上是增函数,试问 上是增函数还是减函数?请证明你的结论。
上是增函数还是减函数?请证明你的结论。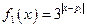 ,
,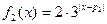 ,
,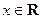 ,
,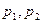 为常
为常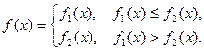
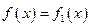 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用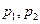 表示);
表示);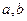 为两实数,
为两实数,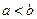 且
且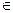
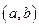 ,若
,若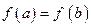
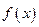 在区间
在区间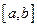 上的单调增区间的长度和为
上的单调增区间的长度和为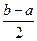 (闭区间
(闭区间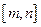 的长度定义为
的长度定义为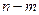 ).
).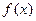 满足关系式
满足关系式 且
且 上是增函数
上是增函数
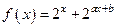 ,且f(1)=
,且f(1)=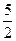 ,f(2)=
,f(2)=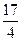 .(1)求
.(1)求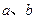 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在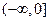 上的单调性,并证明。
上的单调性,并证明。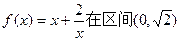 上是减函数.
上是减函数.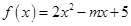 ,
,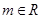 ,它在
,它在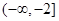 上单调递减,则
上单调递减,则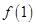 的取值范围是 ( )
的取值范围是 ( )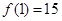
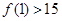

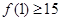
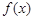 是定义在
是定义在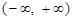 上的偶函数. 当
上的偶函数. 当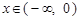 时,
时,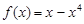 ,
,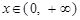 时,
时, .
.