题目内容
(本小题满分14分)若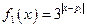 ,
,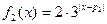 ,
,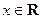 ,
,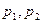 为常
为常
数,且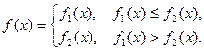
(Ⅰ)求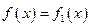 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用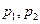 表示);
表示);
(Ⅱ)设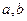 为两实数,
为两实数,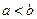 且
且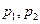
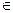
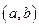 ,若
,若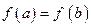
求证: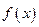 在区间
在区间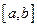 上的单调增区间的长度和为
上的单调增区间的长度和为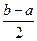 (闭区间
(闭区间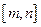 的长度定义为
的长度定义为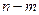 ).
).
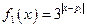 ,
,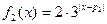 ,
,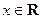 ,
,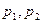 为常
为常数,且
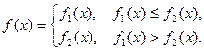
(Ⅰ)求
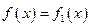 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用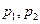 表示);
表示);(Ⅱ)设
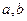 为两实数,
为两实数,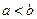 且
且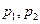
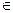
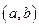 ,若
,若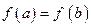
求证:
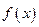 在区间
在区间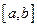 上的单调增区间的长度和为
上的单调增区间的长度和为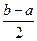 (闭区间
(闭区间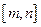 的长度定义为
的长度定义为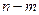 ).
).解:(Ⅰ)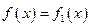 恒成立
恒成立
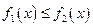
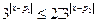
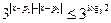 ;
;
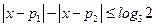 (*)
(*)
因为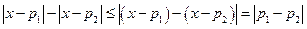 ,
,
所以,故只需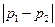
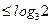 (*)恒成立.
(*)恒成立.
综上所述,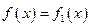 对所有实数成立的充要条件是
对所有实数成立的充要条件是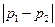
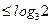 . ………4分
. ………4分
(Ⅱ)1°如果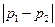
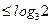 ,则的图象关于直线
,则的图象关于直线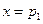 对称.因为
对称.因为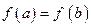 ,所以区间
,所以区间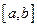 关于直线
关于直线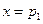 对称.
对称.
因为减区间为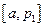 ,增区间为
,增区间为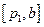 ,所以单调增区间的长度和为
,所以单调增区间的长度和为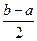 . ………6分
. ………6分
2°如果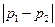
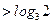 .
.
(1)当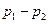
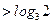 时.
时.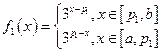 ,
,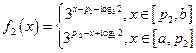
当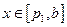 ,
,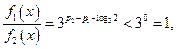 因为
因为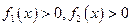 ,所以
,所以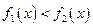 ,故
,故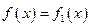 =
=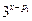 .
.
当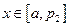 ,
,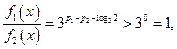 因为
因为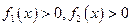 ,所以
,所以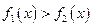 ,故
,故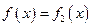 =
=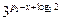 .
.
因为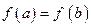 ,所以
,所以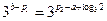 ,所以
,所以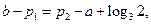 即
即
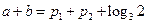 .
.
当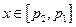 时,令
时,令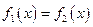 ,则
,则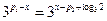 ,所以
,所以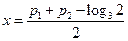 ,
,
当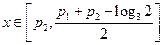 时,
时,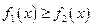 ,所以
,所以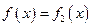 =
=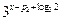 ;
;
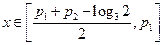 时,
时,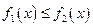 ,所以
,所以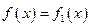 =
=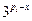 .
.
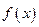 在区间
在区间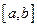 上的单调增区间的长度和
上的单调增区间的长度和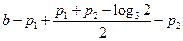
=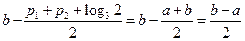 . …………10分
. …………10分
(2)当
 时.
时.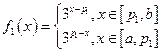 ,
,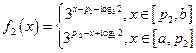
当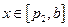 ,
,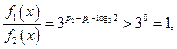 因为
因为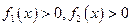 ,所以
,所以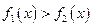 ,故
,故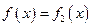 =
=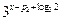 .
.
当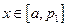 ,
,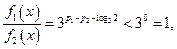 因为
因为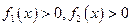 ,所以
,所以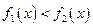 ,故
,故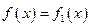 =
=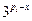 .
.
因为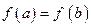 ,所以
,所以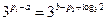 ,所以
,所以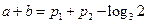 .
.
当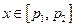 时,令
时,令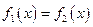 ,则
,则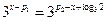 ,所以
,所以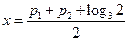 ,
,
当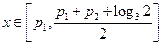 时,
时, 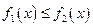 ,所以
,所以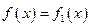 =
=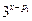 ;
;
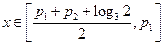 时,
时,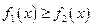 ,所以
,所以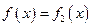 =
=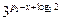 ;
;
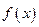 在区间
在区间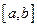 上的单调增区间的长度和
上的单调增区间的长度和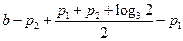
=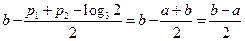 .
.
综上得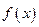 在区间
在区间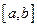 上的单调增区间的长度和为
上的单调增区间的长度和为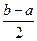 . …………14分
. …………14分
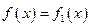 恒成立
恒成立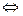
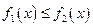
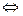
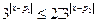
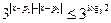 ;
;
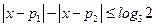 (*)
(*)因为
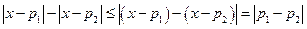 ,
,所以,故只需
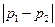
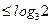 (*)恒成立.
(*)恒成立.综上所述,
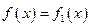 对所有实数成立的充要条件是
对所有实数成立的充要条件是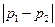
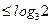 . ………4分
. ………4分 (Ⅱ)1°如果
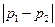
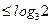 ,则的图象关于直线
,则的图象关于直线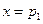 对称.因为
对称.因为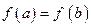 ,所以区间
,所以区间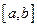 关于直线
关于直线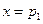 对称.
对称.因为减区间为
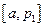 ,增区间为
,增区间为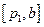 ,所以单调增区间的长度和为
,所以单调增区间的长度和为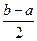 . ………6分
. ………6分2°如果
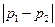
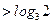 .
.(1)当
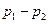
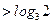 时.
时.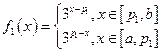 ,
,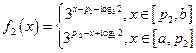
当
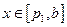 ,
,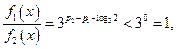 因为
因为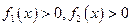 ,所以
,所以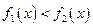 ,故
,故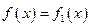 =
=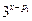 .
.当
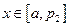 ,
,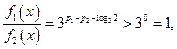 因为
因为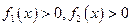 ,所以
,所以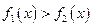 ,故
,故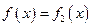 =
=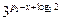 .
.因为
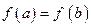 ,所以
,所以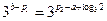 ,所以
,所以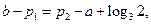 即
即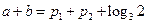 .
.当
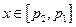 时,令
时,令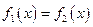 ,则
,则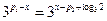 ,所以
,所以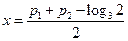 ,
,当
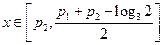 时,
时,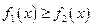 ,所以
,所以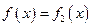 =
=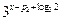 ;
;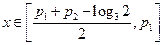 时,
时,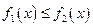 ,所以
,所以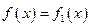 =
=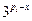 .
.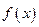 在区间
在区间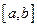 上的单调增区间的长度和
上的单调增区间的长度和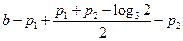
=
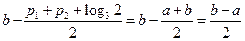 . …………10分
. …………10分(2)当
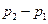
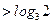 时.
时.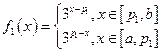 ,
,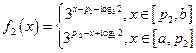
当
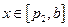 ,
,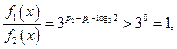 因为
因为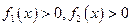 ,所以
,所以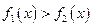 ,故
,故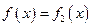 =
=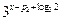 .
.当
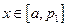 ,
,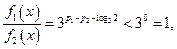 因为
因为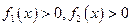 ,所以
,所以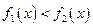 ,故
,故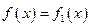 =
=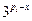 .
.因为
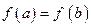 ,所以
,所以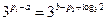 ,所以
,所以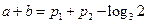 .
.当
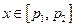 时,令
时,令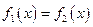 ,则
,则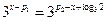 ,所以
,所以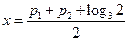 ,
,当
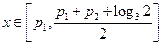 时,
时, 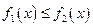 ,所以
,所以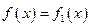 =
=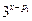 ;
;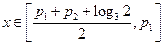 时,
时,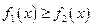 ,所以
,所以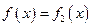 =
=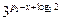 ;
; 在区间
在区间 上的单调增区间的长度和
上的单调增区间的长度和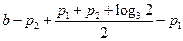
=
 .
.综上得
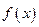 在区间
在区间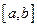 上的单调增区间的长度和为
上的单调增区间的长度和为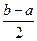 . …………14分
. …………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
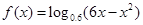 的单调递增区间为( )
的单调递增区间为( )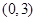
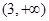


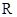 上的奇函数
上的奇函数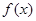 有最小正周期2,且当
有最小正周期2,且当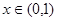 时,
时,
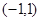 上的解析式; (Ⅱ)判断
上的解析式; (Ⅱ)判断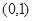 上的单调性;
上的单调性;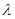 取何值时,方程
取何值时,方程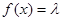 在
在 是定义在R上的奇函数,
是定义在R上的奇函数, ,在
,在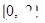 上
上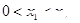 <4且
<4且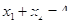 ,则
,则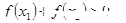 ;
; ,则
,则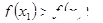 ;
; 内恰有四个不同的解
内恰有四个不同的解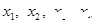 ,则
,则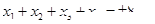 。其中正确的有
。其中正确的有
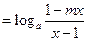 是奇函数(
是奇函数(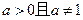 ),
),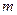 的值
的值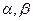 ](
](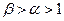 ),判断
),判断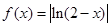 在其上为增函数的是( ▲ ).
在其上为增函数的是( ▲ ).
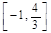
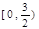

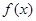 是偶函数,在(-∞,0]上是减函数,则满足
是偶函数,在(-∞,0]上是减函数,则满足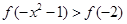 的x的取值范围是
的x的取值范围是 
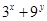 的最小值为
的最小值为 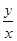 的最大值为 ■
的最大值为 ■