题目内容
已知数列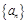 中,
中,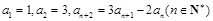 .
.
(1)设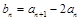 ,求证:数列
,求证:数列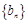 是常数列,并写出其通项公式;
是常数列,并写出其通项公式;
(2)设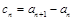 ,求证:数列
,求证:数列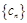 是等比数列,并写出其通项公式;
是等比数列,并写出其通项公式;
(3)求数列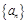 的通项公式.
的通项公式.
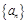 中,
中,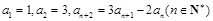 .
.(1)设
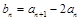 ,求证:数列
,求证:数列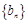 是常数列,并写出其通项公式;
是常数列,并写出其通项公式;(2)设
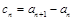 ,求证:数列
,求证:数列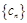 是等比数列,并写出其通项公式;
是等比数列,并写出其通项公式;(3)求数列
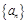 的通项公式.
的通项公式.(1)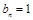 (2)
(2)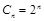 (3)
(3)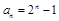
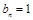 (2)
(2)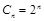 (3)
(3)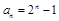
(1)利用常数列的定义即证:bn+1=bn即可.
(2)利用等比数列的定义证明: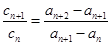 再进一步证明出其比值是一个与n无关的常数即可.
再进一步证明出其比值是一个与n无关的常数即可.
(3)在(2)的基础上,可由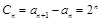 ,通过叠加的方法求an即可
,通过叠加的方法求an即可
(1)证明:∵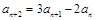 ∴
∴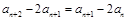 又∵
又∵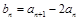
∴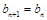 ∴
∴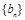 是常数列,且
是常数列,且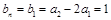 ……………(3分)
……………(3分)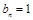 ……(4分)
……(4分)
(2)证明∵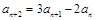 ∴
∴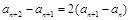 又∵
又∵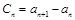 ∴
∴ 而
而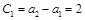 ∴
∴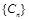 是以2为首项,2为公比的等比数列………………(7分)
是以2为首项,2为公比的等比数列………………(7分)
∴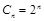 …………(8分)
…………(8分)
(3)解: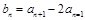 ①
①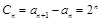 ②
②
②-①得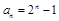
(2)利用等比数列的定义证明:
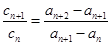 再进一步证明出其比值是一个与n无关的常数即可.
再进一步证明出其比值是一个与n无关的常数即可.(3)在(2)的基础上,可由
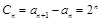 ,通过叠加的方法求an即可
,通过叠加的方法求an即可(1)证明:∵
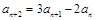 ∴
∴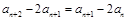 又∵
又∵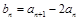
∴
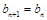 ∴
∴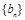 是常数列,且
是常数列,且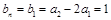 ……………(3分)
……………(3分)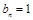 ……(4分)
……(4分)(2)证明∵
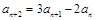 ∴
∴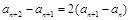 又∵
又∵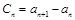 ∴
∴ 而
而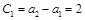 ∴
∴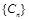 是以2为首项,2为公比的等比数列………………(7分)
是以2为首项,2为公比的等比数列………………(7分)∴
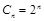 …………(8分)
…………(8分)(3)解:
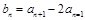 ①
①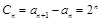 ②
②②-①得
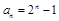

练习册系列答案
相关题目
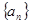 的前
的前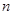 项和为
项和为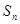 ,等比数列
,等比数列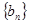 的前
的前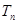 ,它们满足
,它们满足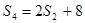 ,
,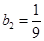 ,
,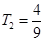 ,且当
,且当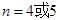 时,
时,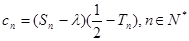 ,如果
,如果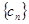 是单调数列,求实数
是单调数列,求实数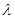 的取值范围.
的取值范围.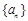 的前n项和为
的前n项和为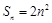 ,
,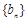 为等比数列,且
为等比数列,且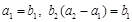 .
.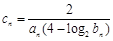 ,求数列
,求数列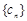 的前n项和
的前n项和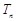 .
. 的前n项和为bn,数列
的前n项和为bn,数列 的前n项积为cn且
的前n项积为cn且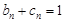 ,则数列
,则数列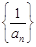 中最接近2012的数是( )
中最接近2012的数是( )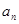 }的首项a1=5,前n项和为Sn,且Sn+1=2Sn+n+5
}的首项a1=5,前n项和为Sn,且Sn+1=2Sn+n+5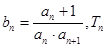 是数列{
是数列{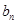 }前n项和,求Tn.
}前n项和,求Tn.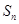 是等差数列
是等差数列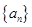 的前
的前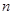 项和,且
项和,且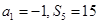 .
.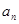 ;
;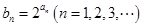 ,计算
,计算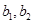 和
和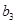 ,由此推测数列
,由此推测数列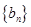 是等差数列还是等比数列,证明你的结论.
是等差数列还是等比数列,证明你的结论.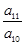 <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为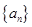 中,
中, ,
,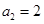 ,
,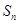 是数列
是数列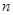 项和,且
项和,且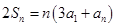 ,
,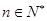 .
. 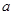 的值;
的值;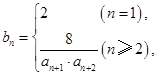
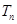 是数列
是数列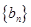 的前
的前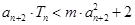 对一切
对一切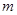 取值范围.
取值范围.
