题目内容
已知定义在区间(0，＋∞)上的函数f(x)满足f(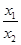)＝f(x1)－f(x2)，且当x>1时，f(x)<0.(1)求f(1)的值；(2)判断f(x)的单调性；(3)若f(3)＝－1，解不等式f(|x|)<－2.
（1）0（2）函数f(x)在区间(0，＋∞)上是减函数（3）{x|x>9或x<－9}
解析
已知一次函数满足。（1）求的解析式；（2）求函数的值域。
已知函数．（1）求函数的最小正周期；（2）判断函数的奇偶性, 并说明理由。
已知函数f(x)＝x|m－x|(x∈R)，且f(4)＝0.(1)求实数m的值；(2)作出函数f(x)的图象并判断其零点个数；(3)根据图象指出f(x)的单调递减区间；(4)根据图象写出不等式f(x)>0的解集；(5)求集合M＝{m|使方程f(x)＝m有三个不相等的实根}．
已知函数f(x)＝x2－4ax＋2a＋6，x∈R.(1)若函数的值域为[0，＋∞)，求a的值；(2)若函数的值域为非负数集，求函数f(a)＝2－a|a＋3|的值域．
已知定义在区间(0，＋∞)上的函数f(x)满足f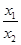＝f(x1)－f(x2)，且当x>1时，f(x)<0.(1)求f(1)的值；(2)判断f(x)的单调性；(3)若f(3)＝－1，求f(x)在[2,9]上的最小值．
已知函数f(x)＝x＋sin x.(1)设P，Q是函数f(x)图像上相异的两点，证明：直线PQ的斜率大于0；(2)求实数a的取值范围，使不等式f(x)≥axcos x在上恒成立．
（2011•山东）某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为立方米，且l≥2r．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为c（c＞3）千元．设该容器的建造费用为y千元．（1）写出y关于r的函数表达式，并求该函数的定义域；（2）求该容器的建造费用最小时的r．
某种树苗栽种时高度为A(A为常数)米，栽种n年后的高度记为f(n)．经研究发现f(n)近似地满足f(n)＝，其中，a，b为常数，n∈N，f(0)＝A．已知栽种3年后该树木的高度为栽种时高度的3倍． （1）栽种多少年后，该树木的高度是栽种时高度的8倍；（2）该树木在栽种后哪一年的增长高度最大．
)＝f(x1)－f(x2)，且当x>1时，f(x)<0.
满足
。
的解析式；
的值域。
．
的最小正周期；
的奇偶性, 并说明理由。
＝f(x1)－f(x2)，且当x>1时，f(x)<0.
上恒成立．
立方米，且l≥2r．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为c（c＞3）千元．设该容器的建造费用为y千元．
，其中
，a，b为常数，n∈N，f(0)＝A．已知栽种3年后该树木的高度为栽种时高度的3倍．