题目内容
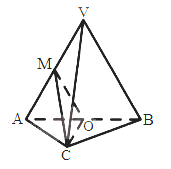
【题目】如图,△ABC中,AB=8,BC=10,AC=6,DB⊥平面ABC,且AE∥FC∥BD,BD=3,FC=4,AE=5,求此几何体的体积.

【答案】96
【解析】试题分析:,取CM=AN=BD,连接DM,MN,DN,用“分割法”把原几何体分割成一个直三棱柱和一个四棱锥.所以V几何体=V三棱柱+V四棱锥.
试题解析:

如图,取CM=AN=BD,连接DM,MN,DN,用“分割法”把原几何体分割成一个直三棱柱和一个四棱锥.所以V几何体=V三棱柱+V四棱锥.由题知三棱柱ABCNDM的体积为V1=![]() ×8×6×3=72.
×8×6×3=72.
四棱锥DMNEF的体积为V2=![]() S梯形MNEF·DN=
S梯形MNEF·DN=![]() ×
×![]() ×(1+2)×6×8=24,
×(1+2)×6×8=24,
则几何体的体积为V=V1+V2=72+24=96.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的 ![]() 城市和交通拥堵严重的
城市和交通拥堵严重的 ![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
(Ⅰ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此 ![]() 列联表,并据此样本分析是否有
列联表,并据此样本分析是否有 ![]() 的把握认为城市拥堵与认可共享单车有关;
的把握认为城市拥堵与认可共享单车有关;
(Ⅱ)若从此样本中的 ![]() 城市和
城市和 ![]() 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自 ![]() 城市的概率是多少?
城市的概率是多少?
附:参考数据:(参考公式: ![]() )
)
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |