题目内容
【题目】如图,在三棱锥V-ABC中,平面VAB![]() 平面ABC,
平面ABC, ![]() VAB为等边三角形,AC
VAB为等边三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分别为AB,VA的中点。
,O,M分别为AB,VA的中点。
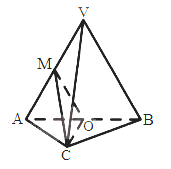
(I)求证:VB//平面MOC;
(II)求证:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱锥V-ABC的体积。
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(III)![]() .
.
【解析】试题分析:(1)由中位线定理得OM//VB,故而VB∥平面MOC;
(2)由等腰三角形三线合一可知OC⊥AB,利用面面垂直的性质得出OC⊥平面VAB,进而证得平面MOC![]() 平面VAB;
平面VAB;
(3)由勾股定理求出AB,OC,得出△VAB的面积,代入棱锥的体积公式即可.
试题解析:
(I)因为O,M分别为AB,VA的中点,
所以OM//VB
又因为VB![]() 平面MOC
平面MOC
所以VB//平面MOC
(II)因为AC=BC,O为AB的中点,
所以OC![]() AB
AB
又因为平面VAB![]() 平面ABC,且OC
平面ABC,且OC![]() 平面ABC,
平面ABC,
所以OC![]() 平面VAB。
平面VAB。
∴平面MOC![]() 平面VAB;
平面VAB;
(III)在等腰直角三角形ACB中,AC=BC=![]() ,
,
所以AB=2,OC=1.
所以等边三角形VAB的面积![]() .
.
又因为CO![]() 平面VAB,
平面VAB,
所以三棱锥C-VAB的体积等于![]() .
.
又因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,
所以三棱锥V-ABC的体积为![]() 。
。

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地早潮叫潮,晚潮叫汐,在通常的情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋。下面是某港口某季节一天的时间与水深的关系表:
时刻( | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
水深/米( | 5 | 7.6 | 5.0 | 2.4 | 5.0 | 7.6 | 5.0 | 2.4 | 5.0 |
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,并分别求出10:00时和13:00时的水深近似数值。
(2)若某船的吃水深度(船底与水面的距离)为4.5米,安全条例规定至少要有1.8米的安全间隙(船底与洋底的距离),该船何时能进入港口,在港口能呆多久?