题目内容
3.函数f(x)=[x]的函数值表示不超过x的最大整数,例如[-3.5]=-4,[2.1]=2,则函数f(x)=[x],x∈[-2,3]与直线y=x(x∈R)的交点个数( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 根据f(x)=[x]的定义,利用分段函数求出函数的解析式,解方程x=[x],x∈[-2,3],即可得到交点个数.
解答 解:根据函数f(x)=[x]的定义可知:
当-2≤x<-1时,f(x)=-2,
当-1≤x<0时,f(x)=-1,
当0≤x<1时,f(x)=0,
当1≤x<2时,f(x)=1,
当2≤x<3时,f(x)=2
当x=3时,f(x)=3,
即f(x)=$\left\{\begin{array}{l}{-2,-2≤x<-1}\\{-1,-1≤x<0}\\{0,0≤x<1}\\{1,1≤x<2}\\{2,2≤x<3}\\{3,x=3}\end{array}\right.$,
由x=[x],x∈[-2,3],可得x=-2,-1,0,1,2,3.
即交点个数为6.
故选:B.
点评 本题主要考查函数解析式的求法,利用函数的定义建立函数关系是解决本题的关键,属于基础题.

练习册系列答案
相关题目
15.下列说法正确的是( )
| A. | 命题“?x∈R,2x>0”的否定是“?x0∈R,2${\;}^{{x}_{0}}$<0” | |
| B. | 命题“若sinx=siny,则x=y”的逆否命题为真命题 | |
| C. | 若命题p,¬q都是真命题,则命题“p∧q”为真命题 | |
| D. | 命题“若△ABC为锐角三角形,则有sinA>cosB”是真命题 |
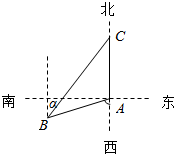 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向在C处追赶上渔船乙,刚好用2小时.则BC=28.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向在C处追赶上渔船乙,刚好用2小时.则BC=28.