题目内容
18.已知函数f(x)=|lnx|,令$a=f({\frac{1}{4}})$,$b=f({\frac{1}{3}})$,c=f(2),则a,b,c的大小关系是a>b>c.分析 由已知可得f($\frac{1}{x}$)=f(x),且当x>1时,f(x)为增函数,进而可得答案.
解答 解:∵函数f(x)=|lnx|,
∴f($\frac{1}{x}$)=|ln$\frac{1}{x}$|=|-lnx|=|lnx|=f(x),
当x>1时,f(x)=|lnx|=lnx为增函数,
∵$a=f({\frac{1}{4}})$=f(4),$b=f({\frac{1}{3}})$=f(3),c=f(2),
∴a>b>c,
故答案为:a>b>c
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
8.△ABC中,sinA:sinB:sinC=3:5:7,则△ABC中最大角的度数是( )
| A. | 150° | B. | 120° | C. | 90° | D. | 135° |
9.已知集合A={x∈N|x<8},则下列关系错误的是( )
| A. | 0∈A | B. | 1.5∉A | C. | -1∉A | D. | 8∈A |
6.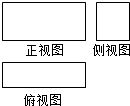 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )| A. | 3$\sqrt{5}$+2 | B. | 6$\sqrt{5}$+4 | C. | 6 | D. | 10 |
3.函数f(x)=[x]的函数值表示不超过x的最大整数,例如[-3.5]=-4,[2.1]=2,则函数f(x)=[x],x∈[-2,3]与直线y=x(x∈R)的交点个数( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
10.若函数f(x)=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点,则k的取值范围是( )
| A. | (0,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{3}{4}$] | C. | [$\frac{1}{2}$,$\frac{3}{4}$) | D. | [$\frac{1}{4}$,1) |