题目内容
15.下列说法正确的是( )| A. | 命题“?x∈R,2x>0”的否定是“?x0∈R,2${\;}^{{x}_{0}}$<0” | |
| B. | 命题“若sinx=siny,则x=y”的逆否命题为真命题 | |
| C. | 若命题p,¬q都是真命题,则命题“p∧q”为真命题 | |
| D. | 命题“若△ABC为锐角三角形,则有sinA>cosB”是真命题 |
分析 写出原命题的否定,可判断A;判断原命题的真假,进而根据互为逆否的两个命题真假性相同,可判断B;根据复合命题真假判断的真值表,可判断C;根据正弦函数的单调性,结合诱导公式,可判断D.
解答 解:命题“?x∈R,2x>0”的否定是“?x0∈R,2${\;}^{{x}_{0}}$≤0”,故错误;
命题“若sinx=siny,则x=y”为假命题,故其逆否命题也为假命题,故错误;
若命题p,¬q都是真命题,则命题q为假命题,则命题“p∧q”为假命题,故错误;
若△ABC为锐角三角形,则A+B$>\frac{π}{2}$,则A$>\frac{π}{2}$-B,则sinA>sin($\frac{π}{2}-B$)=cosB,故正确;
故选:D.
点评 本题考查的知识点是全称命题的否定,四种命题,复合命题,三角函数,难度中档.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
5.连续抛掷两次骰子,所得的点数之和能被3整除的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{11}{36}$ | D. | $\frac{5}{6}$ |
6.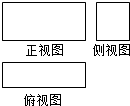 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )| A. | 3$\sqrt{5}$+2 | B. | 6$\sqrt{5}$+4 | C. | 6 | D. | 10 |
3.函数f(x)=[x]的函数值表示不超过x的最大整数,例如[-3.5]=-4,[2.1]=2,则函数f(x)=[x],x∈[-2,3]与直线y=x(x∈R)的交点个数( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
10.若函数f(x)=$\sqrt{-{x}^{2}+4x-3}-kx-k+1$有两个零点,则k的取值范围是( )
| A. | (0,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{3}{4}$] | C. | [$\frac{1}{2}$,$\frac{3}{4}$) | D. | [$\frac{1}{4}$,1) |