题目内容
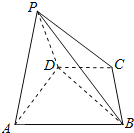
【题目】正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 的中点,则( )
的中点,则( )
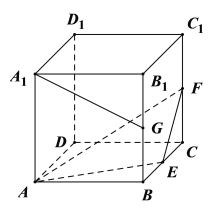
A.直线![]() 与直线
与直线![]() 垂直B.直线
垂直B.直线![]() 与平面
与平面![]() 平行
平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() D.点
D.点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等
的距离相等
【答案】BC
【解析】
A.利用线面垂直的定义进行分析;
B.作出辅助线利用面面平行判断;
C.作出截面然后根据线段长度计算出截面的面积;
D.通过等体积法进行判断.
A.若![]() ,又因为
,又因为![]() 且
且![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() ,显然不成立,故结论错误;
,显然不成立,故结论错误;
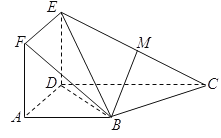
B.如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
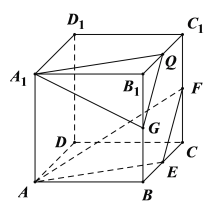
由条件可知:![]() ,
,![]() ,且
,且![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故结论正确;
,故结论正确;
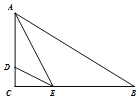
C.如图所示,连接![]() ,延长
,延长![]() 交于点
交于点![]() ,
,
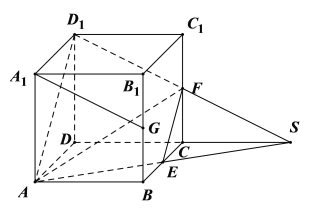
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() 四点共面,
四点共面,
所以截面即为梯形![]() ,又因为
,又因为![]() ,
,![]() ,
,
所以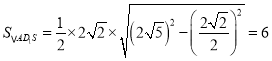 ,所以
,所以![]() ,故结论正确;
,故结论正确;
D.记点![]() 与点
与点![]() 到平面
到平面![]() 的距离分别为
的距离分别为![]() ,
,
因为![]() ,
,
又因为![]() ,
,
所以![]() ,故结论错误.
,故结论错误.
故选:BC.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目