Question

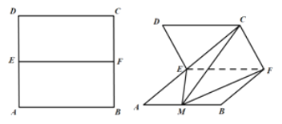
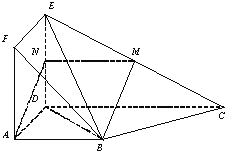
【题目】如图，正方形ADEF与梯形ABCD所在的平面互相垂直，，，，，为的中点．

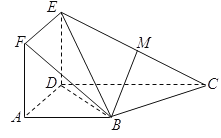
（1）求证：BM∥平面ADEF；

（2）求证：平面BDE⊥平面BEC．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）取DE中点N，连接MN，AN，由三角形中位线定理得，四边形ABMN为平行四边形，即BM∥AN，再由线面平行的判定定理即可得到BM∥平面ADEF；

（2）由已知中正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB＝AD＝2，CD＝4，我们易得到ED⊥BC，解三角形BCD，可得BC⊥BD，由线面垂直的判定定理，可得BC⊥平面BDE，再由面面垂直的判定定理，即可得到平面BDE⊥平面BEC．

（1）取DE中点N，连接MN，AN，在△EDC中，M，N分别为EC，ED的中点

∴MN∥CD，且MN＝CD，由已知AB∥CD，AB＝AD＝2，CD＝4，∴MN∥AB，且MN＝AB

∴四边形ABMN为平行四边形，∴BM∥AN，又∵AN平面ADEF，BM平面ADEF，

∴BM∥平面ADEF.

（2）∵ADEF为正方形，∴ED⊥AD，又∵平面平面，且平面平面，且ED平面ADEF，

∴ED⊥平面ABCD，∴ED⊥BC，在直角梯形ABCD中，AB＝AD＝2，CD＝4，可得BC＝2，

在△BCD中，BD＝BC＝2，CD＝4，∴BC⊥BD，∴BC⊥平面BDE，

又∵BC平面BEC，∴平面BDE⊥平面BEC