题目内容
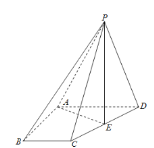
【题目】在四棱锥P﹣ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC![]() AB=2,且平面PAD⊥平面ABCD.
AB=2,且平面PAD⊥平面ABCD.
(1)证明:BD⊥平面PAD
(2)求点C到平面PBD的距离.
【答案】(1)证明见解析 (2)![]() .
.
【解析】
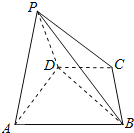
(1)在梯形ABCD中,取AB中点E,连结DE,推导出点D在以AB为直径的圆上,由此能证明BD⊥平面PAD.
(2)取AD中点O,连结PO,则PO⊥AD,设C到平面PBD的距离为h,由VP﹣BCD=VC﹣PBD,能求出点C到平面PBD的距离.
(1)在梯形ABCD中,取AB中点E,连结DE,则DE∥BC,且DE=BC,
故DE![]() ,即点D在以AB为直径的圆上,
,即点D在以AB为直径的圆上,
∴BD⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
BD平面ABCD,∴BD⊥平面PAD.
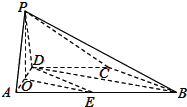
(2)取AD中点O,连结PO,则PO⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD,
由(1)知△ABD和△PBD都是直角三角形,
∴BD![]() 2
2![]() ,
,
∴![]() 2
2![]() ,
,![]() ,
,
解得PO![]() ,
,
设C到平面PBD的距离为h,
由VP﹣BCD=VC﹣PBD,得![]() ,
,
解得h![]() ,
,
∴点C到平面PBD的距离为![]() .
.

练习册系列答案
相关题目