题目内容
8.已知i为虚数单位,“因为任何数的平方都是非负数,-i是个数,所有(-i)2≥0”,这一推理中,产生错误的原因是( )| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 以上答案都不对 |
分析 在“由于任何数的平方都是非负数,-i是个数,所以(-i)2≥0”,”这一推理,写成三段论的形式,再判断大前提“任何数的平方都是非负数”错误,即可得出结论.
解答 解:在“由于任何数的平方都是非负数,-i是个数,所以(-i)2≥0”,”这一推理,写成三段论的形式应是:
任何数的平方都是非负数(大前提),
-i是数(小前提),
所以(-i)2≥0(结论).
由于(-i)2=-4<0,所以结论错误,
原因是大前提“任何数的平方都是非负数”错误,事实上,只有在实数范围内“任何数的平方都是非负数”才正确.
故选:B.
点评 要分析一个演绎推理是否正确,主要观察所给的大前提,小前提和结论及推理形式是否都正确,根据这几个方面都正确,才能得到这个演绎推理正确.

练习册系列答案
相关题目
16.如图是高中课程结构图:音乐所属课程是( )
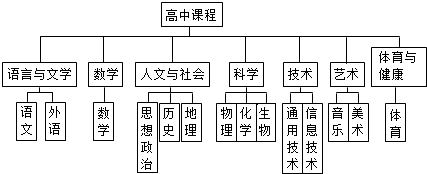

| A. | 艺术 | B. | 人文与社会 | C. | 技术 | D. | 科学 |
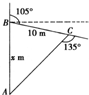 如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m).
如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m). 如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.