题目内容
已知点P (4,4),圆C: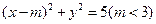 与椭圆E:
与椭圆E: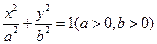 的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线
的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线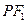 与圆C相切。
与圆C相切。
(1)求m的值与椭圆E的方程;
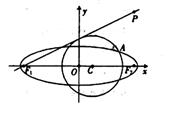
(2)设D为直线PF1与圆C 的切点,在椭圆E上是否存在点Q ,使△PDQ是以PD为底的等腰三角形?若存在,请指出共有几个这样的点?并说明理由。
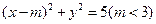 与椭圆E:
与椭圆E: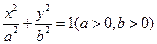 的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线
的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线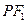 与圆C相切。
与圆C相切。(1)求m的值与椭圆E的方程;
(2)设D为直线PF1与圆C 的切点,在椭圆E上是否存在点Q ,使△PDQ是以PD为底的等腰三角形?若存在,请指出共有几个这样的点?并说明理由。

(1)m=1,椭圆E的方程为
(2)在椭圆上存在两个点Q,使得 PDQ是以PD为底的等边三角形
PDQ是以PD为底的等边三角形

(2)在椭圆上存在两个点Q,使得
 PDQ是以PD为底的等边三角形
PDQ是以PD为底的等边三角形解:(1)∵点A(3,1)在圆上,∴(3-m)2+1="5" 又m<3 ∴m="1" ┉┉2分
设F1(-c,0),∵P(4,4)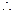 直线PF1方程为4x-(4+c)y+4c="0 " ---------3分
直线PF1方程为4x-(4+c)y+4c="0 " ---------3分
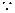 直线PF1与圆C相切,
直线PF1与圆C相切,
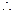 c=4.――――-4分
c=4.――――-4分
由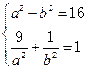 得
得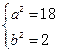
 椭圆E的方程为
椭圆E的方程为 ――――――――6分
――――――――6分
(2)直线PF1方程为4x-8y+16=0,即x-2y+4=0
由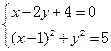 得切点D(0,2)―――――7分
得切点D(0,2)―――――7分
又 P(4,4),
P(4,4),  线段PD中点为M(2,3)―――――8分
线段PD中点为M(2,3)―――――8分
又 椭圆右焦点为F2(4,0),
椭圆右焦点为F2(4,0), 
 ―――10分
―――10分
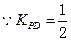 ,
,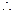 线段PD垂直平分线的斜率为-2 ―――――――11分
线段PD垂直平分线的斜率为-2 ―――――――11分
 ,
,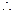 线段PD的垂直平分线与椭圆有两个交点――――13分
线段PD的垂直平分线与椭圆有两个交点――――13分
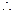 在椭圆上存在两个点Q,使得
在椭圆上存在两个点Q,使得 PDQ是以PD为底的等边三角形―――14分
PDQ是以PD为底的等边三角形―――14分
(或与过点M的椭圆右侧切线斜率比较说明;或用判别式)
设F1(-c,0),∵P(4,4)
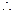 直线PF1方程为4x-(4+c)y+4c="0 " ---------3分
直线PF1方程为4x-(4+c)y+4c="0 " ---------3分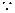 直线PF1与圆C相切,
直线PF1与圆C相切,
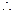 c=4.――――-4分
c=4.――――-4分由
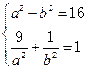 得
得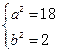
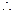 椭圆E的方程为
椭圆E的方程为 ――――――――6分
――――――――6分(2)直线PF1方程为4x-8y+16=0,即x-2y+4=0
由
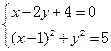 得切点D(0,2)―――――7分
得切点D(0,2)―――――7分又
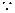 P(4,4),
P(4,4), 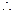 线段PD中点为M(2,3)―――――8分
线段PD中点为M(2,3)―――――8分又
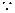 椭圆右焦点为F2(4,0),
椭圆右焦点为F2(4,0), 
 ―――10分
―――10分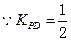 ,
, 线段PD垂直平分线的斜率为-2 ―――――――11分
线段PD垂直平分线的斜率为-2 ―――――――11分 ,
, 线段PD的垂直平分线与椭圆有两个交点――――13分
线段PD的垂直平分线与椭圆有两个交点――――13分 在椭圆上存在两个点Q,使得
在椭圆上存在两个点Q,使得 PDQ是以PD为底的等边三角形―――14分
PDQ是以PD为底的等边三角形―――14分(或与过点M的椭圆右侧切线斜率比较说明;或用判别式)

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
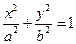 的焦距为
的焦距为 2,离心率为
2,离心率为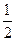 。
。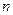 是过原点的直线,
是过原点的直线,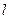 是与
是与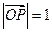 ,是否存在上述直线
,是否存在上述直线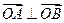 成立?若存在,求出直线
成立?若存在,求出直线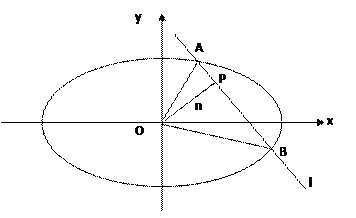
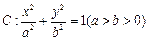 的离心率为
的离心率为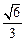 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 .
. 的方程;
的方程;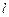 与椭圆
与椭圆 两点,坐标原点
两点,坐标原点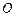 到直线
到直线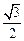 ,求
,求 面积的最大值.
面积的最大值.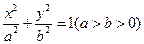 的左焦点为
的左焦点为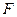 ,左右顶点分别为
,左右顶点分别为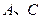 ,上顶点为
,上顶点为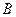 ,过
,过 三点作圆
三点作圆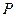 ,其中圆心
,其中圆心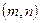 .
. 时,椭圆的离心率的取值范围.
时,椭圆的离心率的取值范围.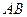 能否和圆
能否和圆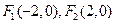 为焦点的椭圆与
为焦点的椭圆与 直线
直线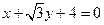 有且仅有一个交点,则椭圆的长轴长为 。
有且仅有一个交点,则椭圆的长轴长为 。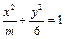 的焦距等于2,则m的值为( )
的焦距等于2,则m的值为( )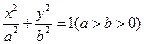 的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且
的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且 是边长为2的正三角形;又椭圆E上的P、Q两点关于直线
是边长为2的正三角形;又椭圆E上的P、Q两点关于直线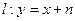 对称.
对称. 过点(
过点(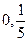 )时,求直线PQ的方程;
)时,求直线PQ的方程;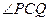 =
=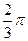 ,求
,求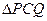 面积的最大值.
面积的最大值.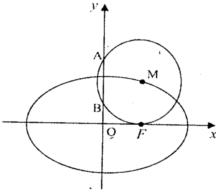
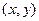 满足
满足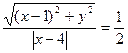 ,则
,则 ( )
( ) 定
定
