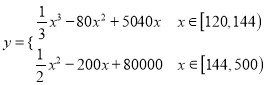题目内容
【题目】下列推理中属于归纳推理且结论正确的是( )
A.由an=2n﹣1,求出S1=12 , S2=22 , S3=32 , …,推断:数列{an}的前n项和Sn=n2
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数
C.由圆x2+y2=r2的面积S=πr2 , 推断:椭圆 ![]() =1的面积S=πab
=1的面积S=πab
D.由(1+1)2>21 , (2+1)2>22 , (3+1)2>23 , …,推断:对一切n∈N* , (n+1)2>2n
【答案】A
【解析】解:对于A,由an=2n﹣1,求出S1=12 , S2=22 , S3=32 , …,推断:数列{an}的前n项和,是由特殊推导出一般性的结论,且 ![]() ,故正确;
,故正确;
对于B,属于演绎推理中的三段论,故不正确;
对于C,是由圆类比椭圆,由圆的面积类比椭圆的面积,故属于类比推理,故不正确;
对于D,属于归纳推理,n=6时,结论不正确,故不正确
故选A.
【考点精析】解答此题的关键在于理解归纳推理的相关知识,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目