Question

【题目】已知函数f（x）=ax2+blnx在x=1处有极值 ．
（1）求a，b的值；
（2）求函数y=f（x）的单调性．

Answer 1

【答案】
（1）解：∵函数f（x）=ax2+blnx，

∴ ，

∵f（x）在x=1处有极值 ，

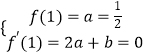∴ ，解得a= ，b=﹣1．

（2）解：由（1）得f（x）= ，其定义域为（0，+∞），

且f′（x）=x﹣ = ．

当x变化时，f′（x），f（x）的变化情况如下表：

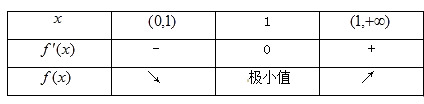
∴函数f（x）的单调减区间是（0，1），单调增区间是（1，+∞）．

【解析】（1）由函数f（x）=ax2+blnx，知 ，由f（x）在x=1处有极值 ，知 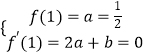，由此能求出a，b的值．（2）由f（x）= ，其定义域为（0，+∞），f′（x）=x﹣ = ．列表讨论，能求出函数f（x）的单调区间．
【考点精析】掌握利用导数研究函数的单调性和函数的极值是解答本题的根本，需要知道一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；极值反映的是函数在某一点附近的大小情况．