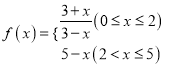题目内容
【题目】已知m∈R,复数z= ![]() +(m2+2m﹣3)i,当m为何值时,
+(m2+2m﹣3)i,当m为何值时,
(1)z∈R;
(2)z是纯虚数;
(3)z对应的点位于复平面第二象限;
(4)(选做)z对应的点在直线x+y+3=0上.
【答案】
(1)解:∵m∈R,复数z= ![]() +(m2+2m﹣3)i为实数,
+(m2+2m﹣3)i为实数,
∴ ![]() ,
,
解得m=﹣3;
(2)解:∵z是纯虚数;
∴ ![]() =0,m2+2m﹣3≠0,
=0,m2+2m﹣3≠0,
解得m=0或m=2;
(3)解:z对应的点位于复平面第二象限;
∴ ![]() <0,m2+2m﹣3>0,
<0,m2+2m﹣3>0,
解得m<﹣3或1<m<2.
(4)解:∵z对应的点在直线x+y+3=0上.
∴ ![]() +(m2+2m﹣3)+3=0,
+(m2+2m﹣3)+3=0,
解得m=0或 ![]() .
.
【解析】(1)由m∈R,复数z= ![]() +(m2+2m﹣3)i为实数,可得
+(m2+2m﹣3)i为实数,可得 ![]() ,解出即可;(2)由z是纯虚数;可得
,解出即可;(2)由z是纯虚数;可得 ![]() =0,m2+2m﹣3≠0,解得m即可;(3)z对应的点位于复平面第二象限;可得
=0,m2+2m﹣3≠0,解得m即可;(3)z对应的点位于复平面第二象限;可得 ![]() <0,m2+2m﹣3>0,解得m即可;(4)由于z对应的点在直线x+y+3=0上,可得
<0,m2+2m﹣3>0,解得m即可;(4)由于z对应的点在直线x+y+3=0上,可得 ![]() +(m2+2m﹣3)+3=0,解得m即可.
+(m2+2m﹣3)+3=0,解得m即可.
【考点精析】利用复数的定义对题目进行判断即可得到答案,需要熟知形如![]() 的数叫做复数,
的数叫做复数,![]() 和
和![]() 分别叫它的实部和虚部.
分别叫它的实部和虚部.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知如表为“五点法”绘制函数f(x)=Asin(ωx+φ)图象时的五个关键点的坐标(其中A>0,ω>0,|φ|<π)
x | ﹣ |
|
|
|
|
f(x) | 0 | 2 | 0 | ﹣2 | 0 |
(Ⅰ)请写出函数f(x)的最小正周期和解析式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.