题目内容
在平面直角坐标系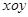 中,已知圆心在
中,已知圆心在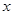 轴上,半径为
轴上,半径为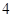 的圆
的圆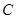 位于
位于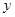 轴的右侧,且与
轴的右侧,且与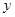 轴相切,
轴相切,
(Ⅰ)求圆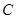 的方程;
的方程;
(Ⅱ)若椭圆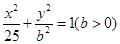 的离心率为
的离心率为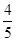 ,且左右焦点为
,且左右焦点为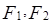 ,试探究在圆
,试探究在圆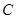 上是否存在点
上是否存在点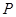 ,使得
,使得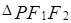 为直角三角形?若存在,请指出共有几个这样的
为直角三角形?若存在,请指出共有几个这样的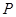 点?并说明理由(不必具体求出这些点的坐标)
点?并说明理由(不必具体求出这些点的坐标)
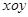 中,已知圆心在
中,已知圆心在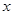 轴上,半径为
轴上,半径为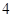 的圆
的圆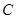 位于
位于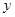 轴的右侧,且与
轴的右侧,且与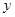 轴相切,
轴相切,(Ⅰ)求圆
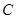 的方程;
的方程;(Ⅱ)若椭圆
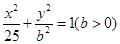 的离心率为
的离心率为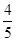 ,且左右焦点为
,且左右焦点为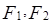 ,试探究在圆
,试探究在圆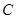 上是否存在点
上是否存在点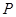 ,使得
,使得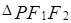 为直角三角形?若存在,请指出共有几个这样的
为直角三角形?若存在,请指出共有几个这样的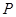 点?并说明理由(不必具体求出这些点的坐标)
点?并说明理由(不必具体求出这些点的坐标)(Ⅰ) ;(Ⅱ),圆
;(Ⅱ),圆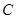 上存在4个点
上存在4个点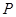 ,使得
,使得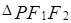 为直角三角形.
为直角三角形.
 ;(Ⅱ),圆
;(Ⅱ),圆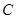 上存在4个点
上存在4个点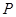 ,使得
,使得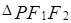 为直角三角形.
为直角三角形.试题分析:(Ⅰ)求圆
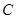 的方程,只要求出圆心与半径即可,而已知圆
的方程,只要求出圆心与半径即可,而已知圆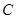 的半径为
的半径为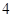 ,圆心在
,圆心在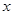 轴上,圆
轴上,圆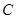 位于
位于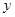 轴的右侧,且与
轴的右侧,且与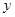 轴相切,故圆心为
轴相切,故圆心为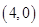 ,从而可得圆
,从而可得圆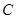 的方程;(Ⅱ)探究在圆
的方程;(Ⅱ)探究在圆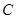 上是否存在点
上是否存在点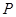 ,使得
,使得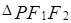 为直角三角形,首先求出
为直角三角形,首先求出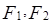 的坐标,而
的坐标,而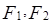 是椭圆
是椭圆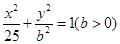 的左右焦点,须求出椭圆的方程,由题意椭圆
的左右焦点,须求出椭圆的方程,由题意椭圆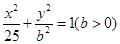 的离心率为
的离心率为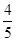 ,
,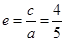 ,可求得,
,可求得,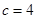 ,可得
,可得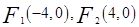 ,
,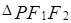 为直角三角形,有圆的方程可知,只需过
为直角三角形,有圆的方程可知,只需过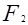 作
作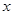 轴的垂线,与圆的两个交点符合题意,过
轴的垂线,与圆的两个交点符合题意,过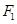 可作圆的两条切线,与圆的两个切点也符合,从而找到
可作圆的两条切线,与圆的两个切点也符合,从而找到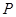 点.
点.试题解析:(Ⅰ)依题意,设圆的方程为(x-a)2+y2=16(a>0). (1分)
∵圆与y轴相切,∴a=4,∴圆的方程为(x-4)2+y2=16 (4分)
(Ⅱ)∵椭圆
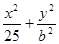 =1的离心率为
=1的离心率为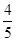 ,∴e=
,∴e=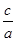 =
=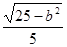 =
=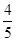
解得b2=9 (6分)
∴c=
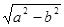 =4,∴F1(-4,0),F2(4,0) (7分)
=4,∴F1(-4,0),F2(4,0) (7分)∴F2(4,0)恰为圆心C (8分)
(i)过
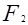 作
作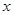 轴的垂线,交圆P1,P2,则∠P1F2F1=∠P2F2F1=90°,符合题意;(10分)
轴的垂线,交圆P1,P2,则∠P1F2F1=∠P2F2F1=90°,符合题意;(10分)(ii)过F1可作圆的两条切线,分别与圆相切于点P3,P4,
连接CP3,CP4,则∠F1P3F2=∠F1P4F2=90°,符合题意. (12分)
综上,圆C上存在4个点P,使得△PF1F2为直角三角形. (13分)

练习册系列答案
相关题目
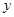 轴截得的弦长为
轴截得的弦长为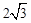 ,圆C的面积小于13.
,圆C的面积小于13.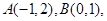 动点P满足
动点P满足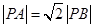 .
.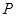 的轨迹为曲线
的轨迹为曲线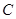 ,求此曲线的方程;
,求此曲线的方程;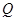 在直线
在直线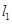 :
: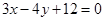 上,直线
上,直线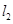 经过点
经过点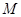 ,求
,求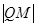 的最小值.
的最小值. 轴的正半轴上,且与
轴的正半轴上,且与 轴相切,则圆的方程是( )
轴相切,则圆的方程是( )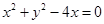



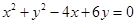 的圆心坐标是( )
的圆心坐标是( )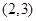
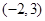
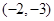
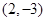
 在圆
在圆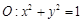 外, 则直线
外, 则直线 与圆
与圆 的位置关系是_______.
的位置关系是_______.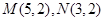 且圆心在直线
且圆心在直线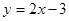 上的圆的方程是________.
上的圆的方程是________.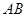 为圆的切线,切点为
为圆的切线,切点为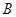 ,点
,点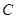 在圆上,
在圆上,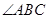 的角平分线
的角平分线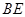 交圆于点
交圆于点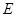 ,
,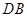 垂直
垂直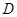 。
。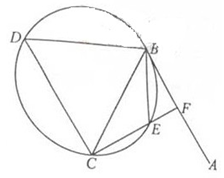
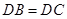 ;
;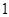 ,
,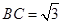 ,延长
,延长 交
交 ,求
,求 外接圆的半径。
外接圆的半径。