题目内容
【题目】如图， 
为圆柱
的母线， 
是底面圆
的直径, 
分别是
的中点, 
(1)证明： 
∥平面
；
(2)求圆柱
的体积和表面积.
【答案】（1）见解析；（2）
， 
.
【解析】试题分析：（1）取
的中点为
，先证明平面
与平面
平行，即可得结论；（2）由
根据勾股定理求出底面圆的直径，进而求得半径，在根据勾股定理可得圆柱的高
，从而由圆柱的体积及侧面积公式可得结果.
试题解析：（1）略
（2）底面半径
， 
，…10分 
， 
【方法点晴】本题主要考查线面平行的判定、面面平行的性质法、圆柱的体积及表面积，属于难题.证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面. 本题（1）是就是利用方法②证明的.
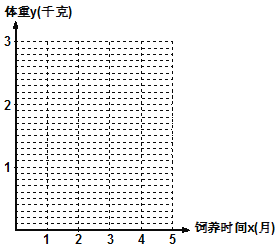
名校课堂系列答案
【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究，在饲料充足的前提下，兴趣小组对饲养时间x(单位：月)与这种鱼类的平均体重y(单位：千克)得到一组观测值，如下表：
|
|
|
|
|
|
|
|
|
|
|
|
(1)在给出的坐标系中，画出关于x、y两个相关变量的散点图．
(2)请根据上表提供的数据，用最小二乘法求出变量
关于变量
的线性回归直线方程
．
(3)预测饲养满12个月时，这种鱼的平均体重(单位：千克)．
（参考公式：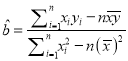 
， 
）
【题目】英州市育才中学对全体教师在教学中是否经常使用信息技术实施教学的情况进行了调查得到统计数据如下(表)
教师教龄 |
|
|
|
|
教师人数 |
|
|
|
|
经常使用信息技术实施教学的人数 |
|
|
|
|
（1）求该校教师在教学中不经常使用信息技术实施教学的概率；
（2）在教龄
年以下，且经常使用信息技术教学的教师中任选
人，其中恰有一人教龄在
年以下的概率是多少？
