题目内容
A、B两个代表队进行乒乓球对抗赛，每队三名队员，A队队员是A1、A2、A3，B队队员是B1、B2、B3。按以往多次比赛的统计，对阵队员之间胜负概率如下：
现按表中对阵方式出场, 每场胜队得1分, 负队得0分,设A队、B队最后总分分别为x、h.
(Ⅰ) 求x、h的概率分布；
(Ⅱ) 求Ex、Eh.
| 对阵队员 | A队队员胜的概率 | A队队员负的概率 |
| A1对B1 | 2 3 | 1 3 |
| A2对B2 | 2 5 | 3 5 |
| A3对B3 | 2 5 | 3 5 |
现按表中对阵方式出场, 每场胜队得1分, 负队得0分,设A队、B队最后总分分别为x、h.
(Ⅰ) 求x、h的概率分布；
(Ⅱ) 求Ex、Eh.
见解析
解：(Ⅰ) x的可能取值分别为3, 2, 1, 0.P(x=" 3)" =
（即A队连胜3场）
P(x=" 2)" =
（即A队共胜2场）
P(x=" 1)" =
（即A队恰胜1场）
P(x=" 0)" =
（即A队连负3场）
根据题意知 x + h = 3，所以
(Ⅱ) Ex =
； 因为x + h = 3，
所以Eh= 3 – Ex=
（即A队连胜3场）P(x=" 2)" =
（即A队共胜2场）P(x=" 1)" =
（即A队恰胜1场）P(x=" 0)" =
（即A队连负3场）根据题意知 x + h = 3，所以
(Ⅱ) Ex =
； 因为x + h = 3，所以Eh= 3 – Ex=
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
是一个离散型随机变量，其分布列如下表：求
值，并求
．
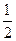
，用随机变量
表示A在1次实验中发生的次数。（1）求方差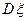
的最大值；（2）求
的最大值。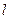
为平面上过点（0，1）的直线，
，
，
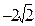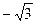，0，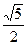
，
，
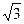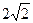，用d表示坐标原点到
