题目内容
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
(Ⅰ)请根据图中所给数据,求出a的值;
(Ⅱ)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(Ⅲ)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[60,70)内的人数,求X的分布列和数学期望.

(Ⅰ)请根据图中所给数据,求出a的值;
(Ⅱ)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(Ⅲ)为了了解学生本次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[60,70)内的人数,求X的分布列和数学期望.

(Ⅰ)根据频率分布直方图中的数据,可得a=
=0.1-0.07=0.03,
所以a=0.03.…(2分)
(Ⅱ)学生成绩在[50,60)内的共有40×0.05=2人,在[60,70)内的共有40×0.225=9人,
成绩在[50,70)内的学生共有11人.…(4分)
设“从成绩在[50,70)的学生中随机选3名,且他们的成绩都在[60,70)内”为事件A,
…(5分)
则P(A)=
=
.…(7分)
所以选取的3名学生成绩都在[60,70)内的概率为
.
(Ⅲ)依题意,X的可能取值是1,2,3.…(8分)P(X=1)=
=
;
P(X=2)=
=
;
P(X=3)=P(A)=
.…(10分)
所以X的分布列为
…(11分)
Eξ=1×
+2×
+3×
=
.…(13分)
| 1-(0.005+0.0075+0.0225+0.035)×10 |
| 10 |
所以a=0.03.…(2分)
(Ⅱ)学生成绩在[50,60)内的共有40×0.05=2人,在[60,70)内的共有40×0.225=9人,
成绩在[50,70)内的学生共有11人.…(4分)
设“从成绩在[50,70)的学生中随机选3名,且他们的成绩都在[60,70)内”为事件A,
…(5分)
则P(A)=
| ||
|
| 28 |
| 55 |
所以选取的3名学生成绩都在[60,70)内的概率为
| 28 |
| 55 |
(Ⅲ)依题意,X的可能取值是1,2,3.…(8分)P(X=1)=
| ||||
|
| 3 |
| 55 |
P(X=2)=
| ||||
|
| 24 |
| 55 |
P(X=3)=P(A)=
| 28 |
| 55 |
所以X的分布列为
| ξ | 1 | 2 | 3 | ||||||
| P |
|
|
|
Eξ=1×
| 3 |
| 55 |
| 24 |
| 55 |
| 28 |
| 55 |
| 27 |
| 11 |

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

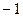 分.(Ⅰ)求拿4次至少得2分的概率; (Ⅱ)求拿4次所得分数
分.(Ⅰ)求拿4次至少得2分的概率; (Ⅱ)求拿4次所得分数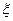 的分布列和数学期望.
的分布列和数学期望.

 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求