题目内容

已知平行四边形ABCD中，
AD
=（2，8），
AB
=（-3，4），对角线AC与BD相交于点M，则
AM
的坐标为（　　）
A、（-
1
2
，6）
B、（-
1
2
，6）
C、（
1
2
，-6）
D、（
1
2
，6）
考点：平面向量坐标表示的应用
专题：平面向量及应用
分析：画出图形，根据向量的平行四边形合成法则，求出
AM
=
1
2
AC
=
1
2
（
AD
+
AB
），即得结果．
解答：解：画出图形，如图所示；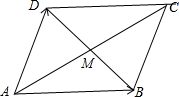
平行四边形ABCD中，
AD
=（2，8），
AB
=（-3，4），
∴
AM
=
1
2
AC
=
1
2
（
AD
+
AB
）=
1
2
（2-3，8+4）=（-
1
2
，6）；
∴
AM
的坐标为（-
1
2
，6）．
故选：B．
点评：本题考查了平面向量的应用问题，解题时应画出图形，结合图形解答问题，是基础题．
练习册系列答案
相关题目
执行如图所示的程序框图，则输出0的概率为（　　）
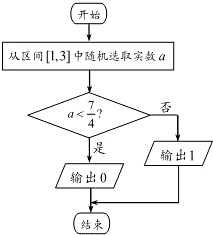
A、
3
8
B、
5
8
C、
1
2
D、
2
3
设集合A={（x，y）|（x-4）2+y2≤16}的元素（x0，y0），则满足y0≥x0的概率是（　　）
A、
1
3
-
1
2π
B、
1
2
-
1
2π
C、
2
3
-
1
2π
D、
1
4
-
1
2π
已知方程
|cosx|
x
=k在（0，+∞）上有两个不同的解α、β（α＜β），则下列的四个命题正确的是（　　）
A、sin2α=2αcos2α
B、cos2α=2αsin2α
C、sin2β=-2βsin2β
D、cos2β=-2βsina2β
已知
a
=（
3
（cosωx+sinωx），sinωx），
b
=（cosωx-sinωx，2cosωx）．函数f（x）=
a
•
b
，其中ω＞0，且f（x）的最小正周期为π．
（Ⅰ） 求f（x）的单调递增区间；
（Ⅱ） 利用五点法作出f（x）在[
π
6
，
5π
6
]上的图象．
若P是锐角△AOB所在的平面内的动点，且
OP
•
OB
=
OA
•
OB
．给出下列命题：
①|
OP
|=|
OA
|恒成立
②|
OP
|的最小值为|
OB
|
③点P的轨迹是一条直线
④存在P使|
PO
+
PB
|=|
OB
|
其中正确的命题个数是（　　）
A、1B、2C、3D、4
当x∈[-
π
2
，
π
2
]时，函数f（x）=sinx+
3
cosx的最大值与最小值分别是（　　）
A、1，-1
B、1，-
1
2
C、2，-2
D、2，-1
若{bn}为等差数列，b2=4，b4=8．数列{an}满足a1=1，bn=an+1-an（n∈N*），则a8=（　　）
A、56B、57C、72D、73
下列命题：
①G2=ab是三个数a、G、b成等比数列的充要条件；
②若y=f（x）不恒为0，且对于?x∈R，都有f（x+2）=-f（x），则f（x）是周期函数；
③对于命题p：?x∈R，2x+3＞0，则￢p：?x0∈R，2x0+3＜0；
④直线l：
2
x+
2
y+1+a=0与圆C：x2+y2=a（a＞0）相离．
其中不正确命题的个数为（　　）
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网