题目内容
已知方程
=k在(0,+∞)上有两个不同的解α、β(α<β),则下列的四个命题正确的是( )
| |cosx| |
| x |
| A、sin2α=2αcos2α |
| B、cos2α=2αsin2α |
| C、sin2β=-2βsin2β |
| D、cos2β=-2βsina2β |
考点:余弦函数的图象
专题:导数的综合应用
分析:将方程
=k转化为|cosx|=kx,作出两个函数的图象,利用数形结合,以及导数的几何意义即可得到结论.
| |cosx| |
| x |
解答: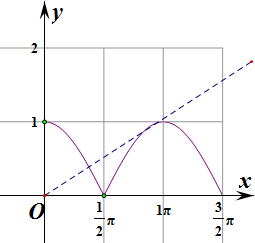 解:∵
解:∵
=k,∴|cosx|=kx,
∴要使方程
=k(k>0)在(0,+∞)上有两个不同的解,则y=|cosx|的图象与直线y=kx(k>0)在(0,+∞)上
有且仅有两个公共点,
所以直线y=kx与y=|cosx|在(
,π)内相切,且切于点(β,-cosβ),此时y=|cosx|=-cosx.
∴切线的斜率为sinβ=
,∴βsinβ=-cosβ,
∴2βsinβsinβ=2sinβcosβ,
∴sin 2β=-2βsin2β,
故选:C.
 解:∵
解:∵| |cosx| |
| x |
∴要使方程
| |cosx| |
| x |
有且仅有两个公共点,
所以直线y=kx与y=|cosx|在(
| π |
| 2 |
∴切线的斜率为sinβ=
| -cosβ |
| β |
∴2βsinβsinβ=2sinβcosβ,
∴sin 2β=-2βsin2β,
故选:C.
点评:本题主要考查函数的零点与方程的根的关系,导数的几何意义,体现了转化的数学思想.

练习册系列答案
相关题目
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )


| A、f(x)=x•tanx | ||
| B、f(x)=x2+1 | ||
C、f(x)=x2+
| ||
| D、f(x)=x3•cosx |
将120°化为弧度为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知平行四边形ABCD中,
=(2,8),
=(-3,4),对角线AC与BD相交于点M,则
的坐标为( )
| AD |
| AB |
| AM |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
已知f(x)=sinπx+cos(πx-
),则f(x)具有性质是( )
| π |
| 6 |
A、图象的一个对称中心为(
| ||
B、图象的一个对称轴为直线x=
| ||
| C、最小正周期为1 | ||
| D、最大值为2,最小值为-2 |
已知命题p:函数y=sin4x是最小正周期为
的周期函数,命题q:函数y=tanx在(
,π)上单调递减,则下列命题为真命题的是( )
| π |
| 2 |
| π |
| 2 |
| A、p∧q |
| B、(¬p)∨q |
| C、(¬p)∧(¬q) |
| D、(¬p)∨(¬q) |