题目内容
【题目】单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( ) 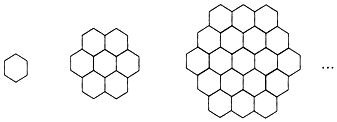
A.37 3n2﹣3n+1
B.38 3n2﹣3n+2
C.36 3n2﹣3n
D.35 3n2﹣3n﹣1
【答案】A
【解析】解:由于f(2)﹣f(1)=7﹣1=6, f(3)﹣f(2)=19﹣7=2×6,
f(4)﹣f(3)=37﹣19=3×6,
f(5)﹣f(4)=61﹣37=4×6,…
因此,当n≥2时,有f(n)﹣f(n﹣1)=6(n﹣1),
所以f(n)=[f(n)﹣f(n﹣1)]+[f(n﹣1)﹣f(n﹣2)]+…+[f(2)﹣f(1)]+f(1)=6[(n﹣1)+(n﹣2)+…+2+1]+1=3n2﹣3n+1.
又f(1)=1=3×12﹣3×1+1,所以f(n)=3n2﹣3n+1.
当n=4时,f(4)=3×42﹣3×4+1=37.
故选:A.
【考点精析】通过灵活运用归纳推理,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理即可以解答此题.

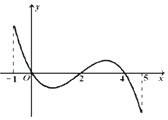
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,
x | ﹣1 | 0 | 4 |
f(x) | 1 | 2 | 2 |
f(x)的导函数y=f′(x)的图象(该图象关于(2,0)中心对称) 如图所示.
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)﹣a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[﹣1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在a=1是上凸的
其中一定正确命题的序号是 .