题目内容
【题目】如图，已知复平面内平行四边形ABCD中，点A对应的复数为﹣1， 
对应的复数为2+2i， 
对应的复数为4﹣4i．
（Ⅰ）求D点对应的复数；
（Ⅱ）求平行四边形ABCD的面积．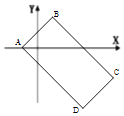
【答案】解：（Ⅰ）依题点A对应的复数为﹣1， 
对应的复数为2+2i， 得A（﹣1，0）， =（2，2），可得B（1，2）．
又 
对应的复数为4﹣4i，得 =（4，﹣4），可得C（5，﹣2）．
设D点对应的复数为x+yi，x，y∈R．
得 
=（x﹣5，y+2）， 
=（﹣2，﹣2）．
∵ABCD 为平行四边形，∴ = ，解得x=3，y=﹣4，
故D点对应的复数为3﹣4i．
（Ⅱ） =（2，2）， =（4，﹣4），
可得： 
=0，∴ 
．
又| |=2 
， 
=4 ．
故平行四边形ABCD的面积= 
=16
【解析】（I）利用复数的几何意义、向量的坐标运算性质、平行四边形的性质即可得出．（II）利用向量垂直与数量积的关系、模的计算公式、矩形的面积计算公式即可得出．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】某品牌连锁便利店有
个分店，A,B,C三种商品在各分店均有销售，这三种商品的单价和重量如表1所示：
商品A | 商品B | 商品C | |
单价（元） | 15 | 20 | 30 |
每件重量（千克） | 0.2 | 0.3 | 0.4 |
表1
某日总店向各分店分配的商品A,B,C的数量如表2所示：
商品 分店 | 分店1 | 分店2 | …… | 分店 |
A | 12 | 20 | m1 | |
B | 15 | 20 | m2 | |
C | 20 | 15 | m3 |
表2
表3表示该日分配到各分店去的商品A,B,C的总价和总重量：
分店1 | 分店2 | …… | 分店 | |
总价（元） |
| |||
总重量（千克） |
|
表3
则
__________ ； 
__________ .
