题目内容
(本大题满分13分)设函数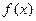 是定义域在
是定义域在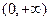 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数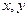 有
有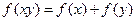 ,已知
,已知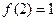 .
.
(1)求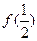 的值;
的值;
(2)一个各项均为正数的数列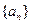 满足:
满足: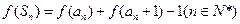 ,其中
,其中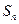 是数列
是数列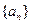 的前n项的和,求数列
的前n项的和,求数列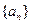 的通项公式;
的通项公式;
(3)在(2)的条件下,是否存在正数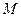 ,使
,使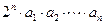

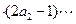
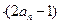 对一切
对一切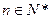 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.
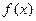 是定义域在
是定义域在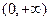 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数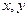 有
有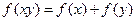 ,已知
,已知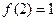 .
.(1)求
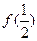 的值;
的值;(2)一个各项均为正数的数列
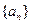 满足:
满足: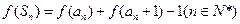 ,其中
,其中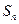 是数列
是数列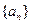 的前n项的和,求数列
的前n项的和,求数列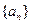 的通项公式;
的通项公式;(3)在(2)的条件下,是否存在正数
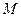 ,使
,使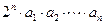

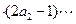
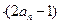 对一切
对一切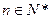 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.(1)-1;
(2) ;
;
(3)存在正数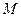 ,使所给定的不等式恒成立,
,使所给定的不等式恒成立,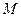 的取值范围为
的取值范围为
(2)
 ;
;(3)存在正数
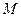 ,使所给定的不等式恒成立,
,使所给定的不等式恒成立,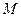 的取值范围为
的取值范围为
(1)∵ ,令
,令 ,有
,有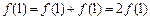 ,∴
,∴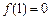 .
.
再令 ,有
,有 ,∴
,∴ ,∴
,∴ …4分
…4分
(2)∵
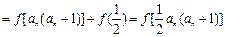 ,
,
又∵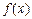 是定义域
是定义域 上单调函数,∵
上单调函数,∵ ,
,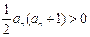 ,
,
∴ ……①
……①
当 时,由
时,由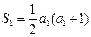 ,得
,得 ,当
,当 时,
时, ……②
……②
由①-②,得 ,
,
化简,得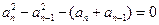 ,∴
,∴ ,
,
∵ ,∴
,∴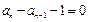 ,即
,即 ,∴数列
,∴数列 为等差数列.
为等差数列.  ,公差
,公差 .
.
∴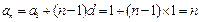 ,故
,故 . ………… 8分
. ………… 8分
(3)∵ ,
,
令 =
= ,
,
而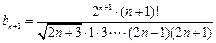 .
.
∴
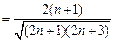 =
= ,
,
∴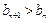 ,数列
,数列 为单调递增函数,由题意
为单调递增函数,由题意 恒成立,则只需
恒成立,则只需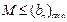 =
= ,
,
∴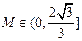 ,存在正数
,存在正数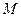 ,使所给定的不等式恒成立,
,使所给定的不等式恒成立, 的取值范围为
的取值范围为 .
.
 ,令
,令 ,有
,有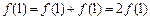 ,∴
,∴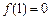 .
.再令
 ,有
,有 ,∴
,∴ ,∴
,∴ …4分
…4分(2)∵

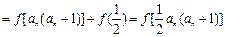 ,
,又∵
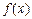 是定义域
是定义域 上单调函数,∵
上单调函数,∵ ,
,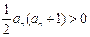 ,
,∴
 ……①
……①当
 时,由
时,由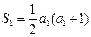 ,得
,得 ,当
,当 时,
时, ……②
……②由①-②,得
 ,
,化简,得
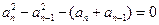 ,∴
,∴ ,
,∵
 ,∴
,∴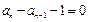 ,即
,即 ,∴数列
,∴数列 为等差数列.
为等差数列.  ,公差
,公差 .
.∴
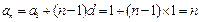 ,故
,故 . ………… 8分
. ………… 8分(3)∵
 ,
,
令
 =
= ,
,而
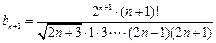 .
. ∴

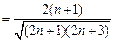 =
= ,
, ∴
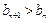 ,数列
,数列 为单调递增函数,由题意
为单调递增函数,由题意 恒成立,则只需
恒成立,则只需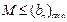 =
= ,
,∴
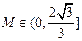 ,存在正数
,存在正数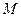 ,使所给定的不等式恒成立,
,使所给定的不等式恒成立,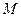 的取值范围为
的取值范围为 .
.
练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 .
.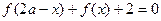 .
.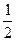 , a+1]时,求f(x)的值域。.
, a+1]时,求f(x)的值域。.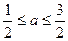 ,求g(x)的最小值.
,求g(x)的最小值.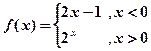 ,那么
,那么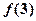 的值是 ( )
的值是 ( ) (-2)
(-2)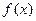 满足
满足
 ,则
,则 。
。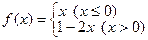 ,则
,则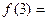 .
.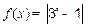 ,
,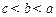 且
且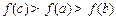 ,则下列关系中一定成立的是
,则下列关系中一定成立的是 ,
, .
.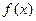 的定义域为实数集,
的定义域为实数集,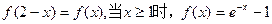 (e为自然对数的底),则必有( )
(e为自然对数的底),则必有( )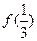 >
> >
>