题目内容
已知函数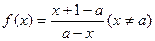 .
.
(1)证明:对定义域内的所有x,都有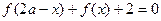 .
.
(2)当f(x)的定义域为[a+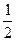 , a+1]时,求f(x)的值域。.
, a+1]时,求f(x)的值域。.
(3)设函数g(x) = x2+| (x-a) f(x) | , 若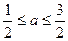 ,求g(x)的最小值.
,求g(x)的最小值.
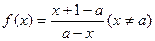 .
.(1)证明:对定义域内的所有x,都有
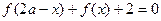 .
.(2)当f(x)的定义域为[a+
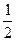 , a+1]时,求f(x)的值域。.
, a+1]时,求f(x)的值域。.(3)设函数g(x) = x2+| (x-a) f(x) | , 若
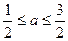 ,求g(x)的最小值.
,求g(x)的最小值.(1)证明略.
(2)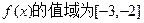 .
.
(3)当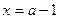 时,g(x)有最小值
时,g(x)有最小值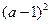
(2)
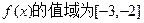 .
.(3)当
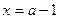 时,g(x)有最小值
时,g(x)有最小值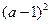
(1)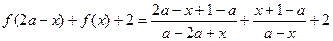
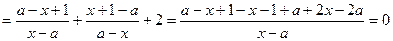 ,
,
∴ 结论成 立. ……………………3分
立. ……………………3分
(2)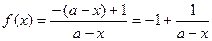 .
.
当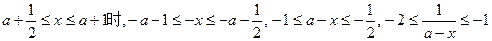 ,
,
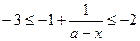 , 即
, 即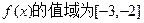 .………………7分
.………………7分
(3)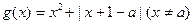 .
.
当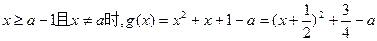 ;
;
当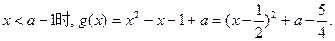
因为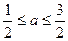 ,所以
,所以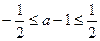 ,则函数
,则函数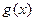 在
在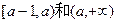 上单调递增, 在
上单调递增, 在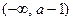 上单调递减,因此,当
上单调递减,因此,当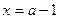 时,g(x)有最小值
时,g(x)有最小值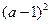 .………12分
.………12分
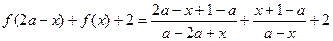
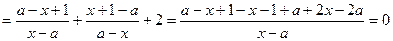 ,
, ∴ 结论成
 立. ……………………3分
立. ……………………3分(2)
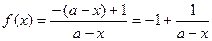 .
.当
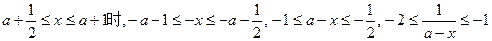 ,
,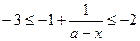 , 即
, 即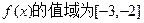 .………………7分
.………………7分(3)
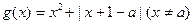 .
.当
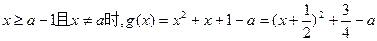 ;
;当
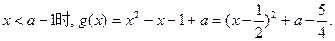
因为
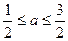 ,所以
,所以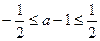 ,则函数
,则函数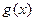 在
在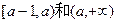 上单调递增, 在
上单调递增, 在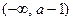 上单调递减,因此,当
上单调递减,因此,当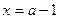 时,g(x)有最小值
时,g(x)有最小值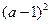 .………12分
.………12分
练习册系列答案
相关题目

 ;⑵若
;⑵若 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。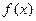 是定义域在
是定义域在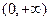 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数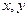 有
有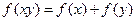 ,已知
,已知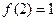 .
.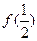 的值;
的值;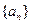 满足:
满足: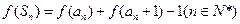 ,其中
,其中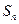 是数列
是数列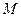 ,使
,使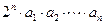

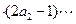
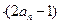 对一切
对一切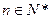 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由. .
. .
.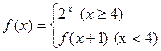 ,则
,则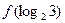 的值为( )
的值为( )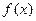 的图象关于点
的图象关于点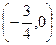 成中心对称,对任意的实数
成中心对称,对任意的实数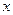 都有
都有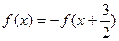 ,且
,且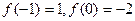 ,则:
,则:




 ,满足
,满足 ,且在区间[0,2]上是减函数,则( )
,且在区间[0,2]上是减函数,则( )


