题目内容
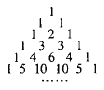
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
A. 110B. 114C. 124D. 125
【答案】B
【解析】
利用二项式系数对应的杨辉上三角形的第![]() 行,令
行,令![]() ,得到二项展开式的二项式系数的和,再结合等差、等比数列的求和公式,即可求解.
,得到二项展开式的二项式系数的和,再结合等差、等比数列的求和公式,即可求解.
由题意,![]() 次二项式系数对应的杨辉三角形的第
次二项式系数对应的杨辉三角形的第![]() 行,
行,
令![]() ,可得二项展开式的二项式系数的和
,可得二项展开式的二项式系数的和![]() ,
,
其中第1行为![]() ,第2行为
,第2行为![]() ,第3行为
,第3行为![]() ,
,![]() 以此类推,
以此类推,
即每一行的数字之和构成首项为1,公比为2的对边数列,
则杨辉三角形中前![]() 行的数字之和为
行的数字之和为![]() ,
,
若除去所有为1的项,则剩下的每一行的数字的个数为![]()
可以看成构成一个首项为1,公差为2的等差数列,则![]() ,
,
令![]() ,解得
,解得![]() ,
,
所以前15项的和表示前7行的数列之和,减去所有的1,即![]() ,
,
即前15项的数字之和为114,故选B.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率是为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率.(结果用分数表示)
个水果是礼品果的概率.(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案![]() :不分类卖出,单价为
:不分类卖出,单价为![]() 元
元![]() .
.
方案![]() :分类卖出,分类后的水果售价如下:
:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/kg) | 16 | 18 | 22 | 24 |
从采购单的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.