题目内容
【题目】如图,已知圆![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,准线的方程为
,准线的方程为![]() ,
,![]() 为抛物线
为抛物线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的两条切线与
的两条切线与![]() 轴交于
轴交于![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若![]() ,求△
,求△![]() 面积
面积![]() 的最小值.
的最小值.
【答案】(1)![]() .
.
(2)32.
【解析】分析:(Ⅰ)根据抛物线的准线方程可得![]() ,故抛物线的方程可求出.
,故抛物线的方程可求出.
(Ⅱ)求出过![]() 的圆的切线
的圆的切线![]() 的方程后可得
的方程后可得![]() 两点的横坐标,它们可用
两点的横坐标,它们可用![]() 及其相应的斜率表示,因此
及其相应的斜率表示,因此![]() 也与这三者相关.再利用圆心到直线的距离为半径得到斜率满足的方程,利用韦达定理和
也与这三者相关.再利用圆心到直线的距离为半径得到斜率满足的方程,利用韦达定理和![]() 消元后可用关于
消元后可用关于![]() 的函数表示
的函数表示![]() ,求出该函数的最小值即可.
,求出该函数的最小值即可.
详解:(Ⅰ)设抛物线![]() 的方程为
的方程为![]() ,
,
则![]() ,∴
,∴![]() ,所以抛物线
,所以抛物线![]() 的方程是
的方程是![]() .
.
(Ⅱ)设切线![]() ,即
,即![]() ,
,
切线与![]() 轴交点为
轴交点为![]() ,圆心到切线的
,圆心到切线的
距离为![]() ,化简得
,化简得![]()
设两切线斜率分别为![]() ,则
,则![]()
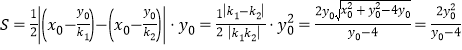
=![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
所以切线与![]() 轴围成的三角形面积
轴围成的三角形面积![]() 的最小值为32.
的最小值为32.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目

