题目内容
已知函数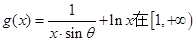 上为增函数,且
上为增函数,且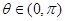 ,
,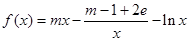 ,
,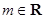 .
.
(1)求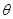 的值;
的值;
(2)当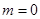 时,求函数
时,求函数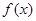 的单调区间和极值;
的单调区间和极值;
(3)若在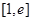 上至少存在一个
上至少存在一个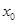 ,使得
,使得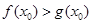 成立,求
成立,求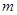 的取值范围.
的取值范围.
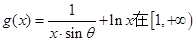 上为增函数,且
上为增函数,且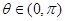 ,
,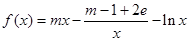 ,
,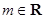 .
.(1)求
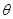 的值;
的值;(2)当
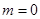 时,求函数
时,求函数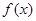 的单调区间和极值;
的单调区间和极值;(3)若在
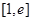 上至少存在一个
上至少存在一个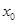 ,使得
,使得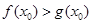 成立,求
成立,求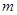 的取值范围.
的取值范围.(1)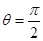 ;
;
(2)函数的单调递增区间是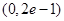 ,递减区间为
,递减区间为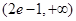 ,极大值
,极大值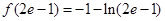 ;
;
(3)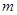 的取值范围为
的取值范围为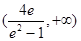 .
.
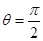 ;
;(2)函数的单调递增区间是
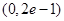 ,递减区间为
,递减区间为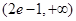 ,极大值
,极大值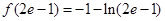 ;
;(3)
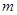 的取值范围为
的取值范围为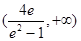 .
.试题分析:(1)利用
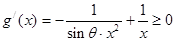 在
在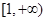 上恒成立,
上恒成立,转化成
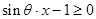 在
在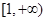 上恒成立,从而只需
上恒成立,从而只需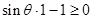 ,
,即
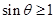 ,结合正弦函数的有界性,得到
,结合正弦函数的有界性,得到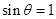 ,求得
,求得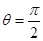 ;
; (2)研究函数的单调性、极值,一般遵循“求导数,求驻点,讨论区间导数值的正负,确定单调性及极值”,利用“表解法”,往往形象直观,易于理解.
(3)构造函数
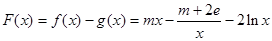 ,
,讨论
 ,
,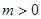 时,
时,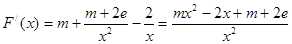 的取值情况,根据
的取值情况,根据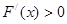 在
在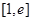 上恒成立,得到
上恒成立,得到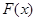 在
在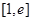 上单调递增,利用
上单调递增,利用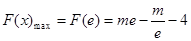 大于0,求得
大于0,求得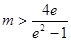 .
.试题解析:(1)由已知
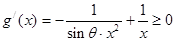 在
在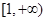 上恒成立,
上恒成立,即
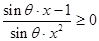 ,∵
,∵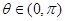 ,∴
,∴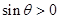 ,
,故
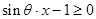 在
在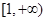 上恒成立,只需
上恒成立,只需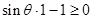 ,
,即
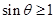 ,∴只有
,∴只有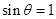 ,由
,由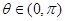 知
知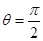 ; 4分
; 4分(2)∵
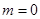 ,∴
,∴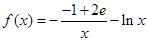 ,
,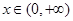 ,
,∴
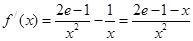 ,
,令
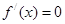 ,则
,则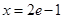
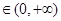 ,
,∴
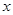 ,
,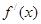 和
和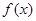 的变化情况如下表:
的变化情况如下表: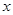 | 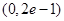 | 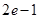 | 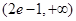 |
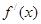 | + | 0 | 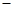 |
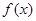 |  | 极大值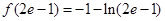 |  |
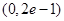 ,递减区间为
,递减区间为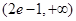 ,有极大值
,有极大值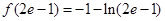 ;
;7分
(3)令
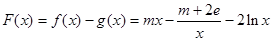 ,
,当
 时,由
时,由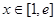 有
有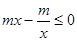 ,且
,且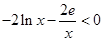 ,
,∴此时不存在
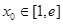 使得
使得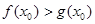 成立;
成立;当
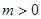 时,
时,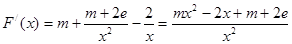 ,
,∵
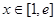 ,∴
,∴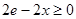 ,又
,又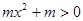 ,∴
,∴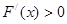 在
在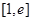 上恒成立,
上恒成立,故
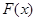 在
在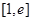 上单调递增,∴
上单调递增,∴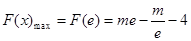 ,
,令
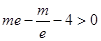 ,则
,则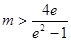 ,
,故所求
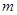 的取值范围为
的取值范围为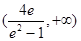 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
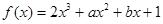 的导数为
的导数为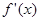 ,若函数
,若函数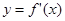 的图象关于直线
的图象关于直线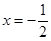 对称,且函数
对称,且函数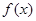 在
在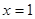 处取得极值.
处取得极值.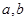 的值;
的值;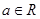 ,函数
,函数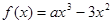 .
.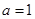 ,求函数
,求函数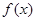 的极值与单调区间;
的极值与单调区间;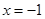 处的切线与直线
处的切线与直线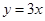 平行,求
平行,求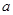 的值;
的值;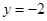 有三个公共点,求
有三个公共点,求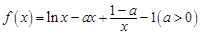 .
.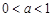 ,试讨论
,试讨论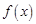 单调性;
单调性;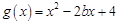 ,当
,当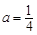 时,若
时,若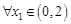 ,存在
,存在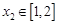 ,使
,使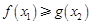 ,求实数
,求实数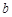 的
的 x2-ln x的单调减区间是 ( ).
x2-ln x的单调减区间是 ( ).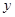 (单位:万元)与年产量
(单位:万元)与年产量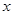 (单位:万件)的函数关系式为
(单位:万件)的函数关系式为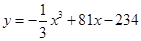 ,则使该生产厂家获得最大年利润的年产量为( )
,则使该生产厂家获得最大年利润的年产量为( )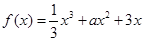 在(0, 1)上不是单调函数,则实数
在(0, 1)上不是单调函数,则实数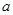 的取值范围为 _____.
的取值范围为 _____.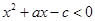 的解集为
的解集为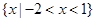 ,且函数
,且函数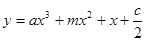 在区间
在区间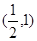 上不是单调函数,则实数
上不是单调函数,则实数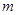 的取值范围为 ( )
的取值范围为 ( )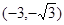
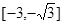
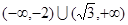
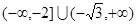
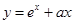 有大于零的极值点,则
有大于零的极值点,则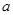 的取值范围是_________.
的取值范围是_________.