题目内容
已知R上的不间断函数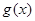 满足:①当
满足:①当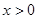 时,
时,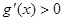 恒成立;②对任意的
恒成立;②对任意的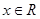 都有
都有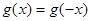 。又函数
。又函数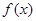 满足:对任意的
满足:对任意的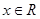 ,都有
,都有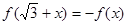 成立,当
成立,当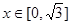 时,
时,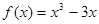 。若关于
。若关于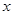 的不等式
的不等式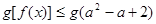 对
对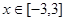 恒成立,则
恒成立,则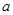 的取值范围( )
的取值范围( )
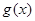 满足:①当
满足:①当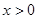 时,
时,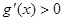 恒成立;②对任意的
恒成立;②对任意的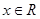 都有
都有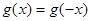 。又函数
。又函数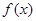 满足:对任意的
满足:对任意的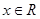 ,都有
,都有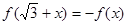 成立,当
成立,当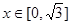 时,
时,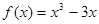 。若关于
。若关于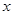 的不等式
的不等式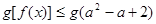 对
对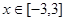 恒成立,则
恒成立,则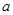 的取值范围( )
的取值范围( )A.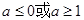 | B.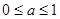 |
C.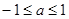 | D.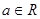 |
A
因为函数g(x)满足:当x>0时,g’(x)>0恒成立,
且对任意x∈R都有g(x)=g(-x),
则函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,
且有g|(x|)=g(x),
所以g[f(x)]≤g(a2-a+2)在R上恒成立,
∴|f(x)|≤|a2-a+2|对x∈∈[-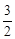 -2
-2 ,
,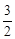 -2
-2 ]恒成立,
]恒成立,
只要使得定义域内|f(x)|max≤|a2-a+2|min,
由于当x∈[- ,
, ]时,f(x)=x3-3x,
]时,f(x)=x3-3x,
求导得:f′(x)=3x2-3=3(x+1)(x-1),
该函数过点(- ,0),(0,0),(
,0),(0,0),( ,0),
,0),
且函数在x=-1处取得极大值f(-1)=2,
在x=1处取得极小值f(1)=-2,
又由于对任意的x∈R都有f( +x)=-f(x),
+x)=-f(x),
∴f(2 +x)=-f(
+x)=-f( +x)=f(x)成立,则函数f(x)为周期函数且周期为T=2
+x)=f(x)成立,则函数f(x)为周期函数且周期为T=2 ,
,
所以函数f(x)在x∈[-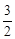 -2
-2 ,
,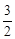 -2
-2 ]的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.
]的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.
故选A
且对任意x∈R都有g(x)=g(-x),
则函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,
且有g|(x|)=g(x),
所以g[f(x)]≤g(a2-a+2)在R上恒成立,
∴|f(x)|≤|a2-a+2|对x∈∈[-
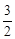 -2
-2 ,
,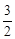 -2
-2 ]恒成立,
]恒成立,只要使得定义域内|f(x)|max≤|a2-a+2|min,
由于当x∈[-
 ,
, ]时,f(x)=x3-3x,
]时,f(x)=x3-3x,求导得:f′(x)=3x2-3=3(x+1)(x-1),
该函数过点(-
 ,0),(0,0),(
,0),(0,0),( ,0),
,0),且函数在x=-1处取得极大值f(-1)=2,
在x=1处取得极小值f(1)=-2,
又由于对任意的x∈R都有f(
 +x)=-f(x),
+x)=-f(x),∴f(2
 +x)=-f(
+x)=-f( +x)=f(x)成立,则函数f(x)为周期函数且周期为T=2
+x)=f(x)成立,则函数f(x)为周期函数且周期为T=2 ,
,所以函数f(x)在x∈[-
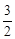 -2
-2 ,
,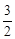 -2
-2 ]的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.
]的最大值为2,所以令2≤|a2-a+2|解得:a≥1或a≤0.故选A

练习册系列答案
相关题目
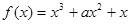 在
在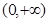 内有两个极值点,则实数
内有两个极值点,则实数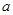 的取值范围是 ( )
的取值范围是 ( )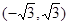
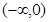
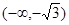
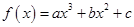 ,其导数f’(x)的图象如图所示,则函数
,其导数f’(x)的图象如图所示,则函数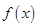 的极小值是 ( )
的极小值是 ( )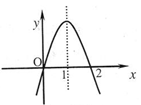
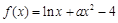 在
在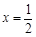 处取得极值,若
处取得极值,若 ,则
,则 的最大值是____________.
的最大值是____________.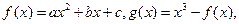 (
(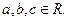 )若
)若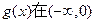 上是增函数,在(0,1)上是减函数,函数
上是增函数,在(0,1)上是减函数,函数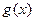 在R上有三个零点,且1是其中一个零点。
在R上有三个零点,且1是其中一个零点。 最小值的取值范围。
最小值的取值范围。
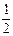
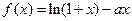 的图象在
的图象在 处的切线与直线
处的切线与直线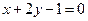 平行.
平行.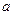 的值;
的值;
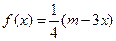 在
在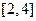 上有两个不相等的实数根,
上有两个不相等的实数根,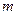 的取值范围;(参考数据:
的取值范围;(参考数据: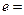 2.71 828…)
2.71 828…)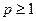 ,数列
,数列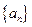 满足
满足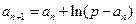 (
( ),
),  ,求证:
,求证: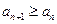 .
.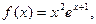
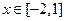 的最大值为 。
的最大值为 。