题目内容
8.设a,b,c都是正数,求证:(1)($\frac{a}{b}$)2+($\frac{b}{a}$)2≥$\frac{a}{b}$+$\frac{b}{a}$;
(2)$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$≥$\frac{3}{2}$;
(3)$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≤$\frac{{a}^{8}+{b}^{8}+{c}^{8}}{{a}^{3}{b}^{3}{c}^{3}}$.
分析 (1)通过作差、变形可知($\frac{a}{b}$)2+($\frac{b}{a}$)2-($\frac{a}{b}$+$\frac{b}{a}$)=$\frac{1}{{a}^{2}{b}^{2}}$(a-b)(a3-b3),利用a、b>0可知a-b与a3-b3同号,进而可得结论;
(2)通过变形、利用($\frac{a}{b+c}$+1)+($\frac{b}{c+a}$+1)+($\frac{c}{a+b}$+1)=(a+b+c)($\frac{1}{b+c}$+$\frac{1}{c+a}$+$\frac{1}{a+b}$)及柯西不等式计算即得结论;
(3)利用a8+a8+b8+b8+b8+c8+c8+c8≥8$\root{8}{{a}^{16}{b}^{24}{c}^{24}}$、相加整理即得结论.
解答 证明:(1)($\frac{a}{b}$)2+($\frac{b}{a}$)2-($\frac{a}{b}$+$\frac{b}{a}$)
=$\frac{a}{b}$($\frac{a}{b}$-1)+$\frac{b}{a}$($\frac{b}{a}$-1)
=$\frac{a}{b}$•$\frac{a-b}{b}$+$\frac{b}{a}$•$\frac{b-a}{a}$
=(a-b)($\frac{a}{{b}^{2}}$-$\frac{b}{{a}^{2}}$)
=$\frac{1}{{a}^{2}{b}^{2}}$(a-b)(a3-b3),
∵a、b>0,
∴a-b与a3-b3同号,
∴$\frac{1}{{a}^{2}{b}^{2}}$(a-b)(a3-b3)>0,
即($\frac{a}{b}$)2+($\frac{b}{a}$)2≥$\frac{a}{b}$+$\frac{b}{a}$;
(2)∵$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$+3
=($\frac{a}{b+c}$+1)+($\frac{b}{c+a}$+1)+($\frac{c}{a+b}$+1)
=(a+b+c)($\frac{1}{b+c}$+$\frac{1}{c+a}$+$\frac{1}{a+b}$)
=$\frac{1}{2}$[(b+c)+(c+a)+(a+b)]($\frac{1}{b+c}$+$\frac{1}{c+a}$+$\frac{1}{a+b}$)
≥$\frac{1}{2}$(1+1+1)2
=$\frac{9}{2}$,
∴$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$+3≥$\frac{9}{2}$,
∴$\frac{a}{b+c}$+$\frac{b}{c+a}$+$\frac{c}{a+b}$≥$\frac{3}{2}$;
(3)∵2a8+3b8+3c8
=a8+a8+b8+b8+b8+c8+c8+c8
≥8$\root{8}{{a}^{16}{b}^{24}{c}^{24}}$
=8a2b3c3,
∴2a8+3b8+3c8≥8a2b3c3,
同理可得:3a8+2b8+3c8≥8a3b2c3,3a8+3b8+2c8≥8a3b3c2,
相加得:8(a8+b8+c8)≥8(a2b3c3+a3b2c3+a3b3c2),
整理得:a8+b8+c8≥($\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$)a3b3c3,
即$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$≤$\frac{{a}^{8}+{b}^{8}+{c}^{8}}{{a}^{3}{b}^{3}{c}^{3}}$.
点评 本题考查不等式的证明,涉及不等式的性质、柯西不等式等基础知识,注意解题方法的积累,属于难题.

| A. | $\overline{z}$=-1-i | B. | |$\overline{z}$|=$\sqrt{2}$ | C. | |$\overline{z}$|=2 | D. | $\overline{z}$=-1+i |
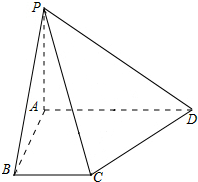 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.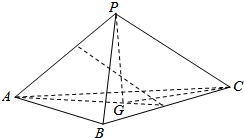 三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点).
三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点). 如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.
如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.
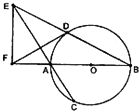 如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.