题目内容
已知动点
 到定点
到定点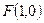 的距离与到定直线
的距离与到定直线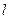 :
: 的距离相等,点C在直线
的距离相等,点C在直线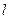 上。
上。(1)求动点
 的轨迹方程。
的轨迹方程。(2)设过定点
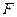 ,且法向量
,且法向量 的直线与(1)中的轨迹相交于
的直线与(1)中的轨迹相交于 两点且点
两点且点 在
在 轴的上方。判断
轴的上方。判断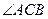 能否为钝角并说明理由。进一步研究
能否为钝角并说明理由。进一步研究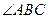 为钝角时点
为钝角时点 纵坐标的取值范围。
纵坐标的取值范围。
解(1)动点
 到定点
到定点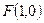 的距离与到定直线
的距离与到定直线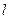 :
: 的距离相等,所以
的距离相等,所以 的轨迹是以点
的轨迹是以点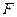 为焦点,直线
为焦点,直线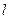 为准线的抛物线,轨迹方程为
为准线的抛物线,轨迹方程为 (4分)
(4分)(2)方法一:由题意,直线
 的方程为
的方程为 (5分)
(5分)故A、B两点的坐标满足方程组
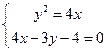
得
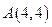 ,
,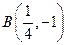
设
 ,则
,则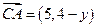 ,
,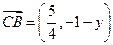 (8分)
(8分)由
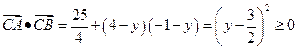 ,所以
,所以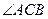 不可能为钝角。(10分)
不可能为钝角。(10分)若
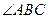 为钝角时,
为钝角时,
 ,
,
 得
得

若
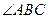 为钝角时,点C纵坐标的取值范围是
为钝角时,点C纵坐标的取值范围是
 (13分)
(13分)注:忽略
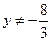 扣1分
扣1分方法二:由题意,直线
 的方程为
的方程为 (5分)
(5分)故A、B两点的坐标满足方程组
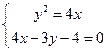 得
得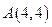 ,
,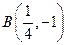
设
 ,则
,则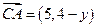 ,
,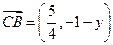 (8分)
(8分)由
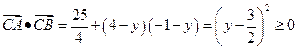 ,所以
,所以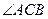 不可能为钝角。(10分)
不可能为钝角。(10分)过
 垂直于直线
垂直于直线 的直线方程为
的直线方程为 令
令 得
得
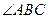 为钝角时,点C纵坐标的取值范围是
为钝角时,点C纵坐标的取值范围是
 (13分)
(13分)注:忽略
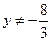 扣1分
扣1分
练习册系列答案
相关题目
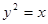 的焦点F,交抛物线于A,B两点,且点A在x轴上方,若直线l的倾斜角
的焦点F,交抛物线于A,B两点,且点A在x轴上方,若直线l的倾斜角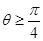 ,则|FA|的取值范围是( )
,则|FA|的取值范围是( )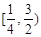
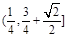
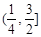
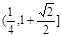
 ,设抛物线
,设抛物线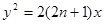 ,过
,过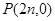 任作直线
任作直线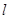 交抛物线于
交抛物线于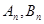 两点,则数列
两点,则数列 的前
的前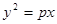 的焦点与椭圆
的焦点与椭圆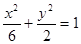 的右焦点重合,则p的值为
的右焦点重合,则p的值为

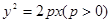 的焦点为
的焦点为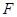 ,
, 过
过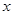 轴的垂线交抛物线于
轴的垂线交抛物线于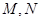 两点.有下列四个命题:①
两点.有下列四个命题:① 必为直角三角形;②
必为直角三角形;②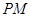 必与抛物线相切;④直线
必与抛物线相切;④直线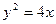 的焦点,且以
的焦点,且以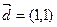 为方向向量的直线的方程是 .
为方向向量的直线的方程是 .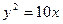 的焦点到准线的距离是( )
的焦点到准线的距离是( )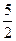
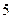
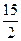
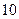
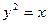 与直线
与直线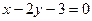 所围成的图形的面积=________.
所围成的图形的面积=________.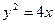 上一点P引抛物线准线的垂线,垂足为M,且
上一点P引抛物线准线的垂线,垂足为M,且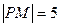 ,设抛物线的焦点为F,则△MPF的面积为
,设抛物线的焦点为F,则△MPF的面积为