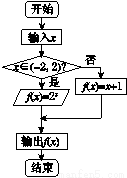
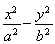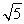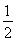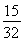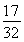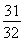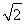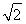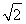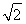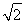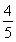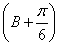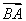题目内容
在直角梯形ABCD中,AB⊥AD,AB∥CD,AD=DC=1,AB=3,动点P在ABCD内运动(含边界),设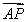 =α·
=α· +β·
+β·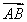 ,则α+β的最大值是( )
,则α+β的最大值是( )
A. 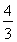 B.
B. 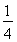 C.1 D.
C.1 D. 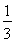
A
【解析】建立如图所示的坐标系,

则B(3,0),C(1,1),D(0,1),设P(x,y),则(x,y)=α(0,1)+β(3,0)=(3β,α),所以x=3β,y=α,所以α+β=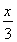 +y,α+β的几何意义是直线y=-
+y,α+β的几何意义是直线y=-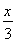 +(α+β)在y轴上的截距,根据线性规划方法,显然在点C处,目标函数取得最大值,这个最大值是
+(α+β)在y轴上的截距,根据线性规划方法,显然在点C处,目标函数取得最大值,这个最大值是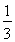 +1=
+1=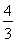 .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目