题目内容
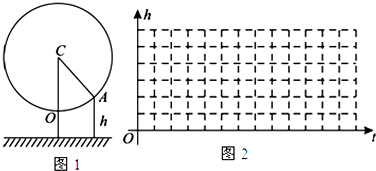
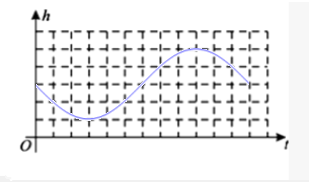
6.如图1,某大风车的半径为2米,每12秒沿逆时针方向匀速旋转一周,它的最低点O离地面1米.风车圆周上一点A从最低点O开始,运动t秒后与地面距离为h米.(1)直接写出函数h=f(t)的关系式,并在给出的坐标系中用五点作图法作出h=f(t)在[0,12)上的图象(要列表,描点);
(2)A从最低点O开始,沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?
分析 (1)通过题意直接得h=f(t)=3-2$cos\frac{π}{6}t$,利用五点作图法即可;
(Ⅱ)通过3-2$cos\frac{π}{6}t$>4,计算可得4<t<8.
解答 解:(1)h=f(t)=3-2$cos\frac{π}{6}t$,
列表:
| $\frac{π}{6}t$ | 0 | $\frac{π}{2}$ | π | $\frac{3}{2}π$ | 2π |
| t | 0 | 3 | 6 | 9 | 12 |
| f(t) | 3 | 1 | 5 | 1 | 3 |
(Ⅱ)∵3-2$cos\frac{π}{6}t$>4,
∴$cos\frac{π}{6}t$<-$\frac{1}{2}$,
又∵$\frac{2π}{3}$<$\frac{π}{6}t$<$\frac{4}{3}π$,t∈[0,12],
∴4<t<8,
所以有4秒钟的时间离地面的高度超过4米.
注:用几何图形求解亦可.
点评 本题考查三角函数在实际问题中的应用,考查五点作图法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
20.已知随机变量ξ的分布列如表,则ξ的标准差等于$\sqrt{3.56}$.
| ξ | 1 | 3 | 5 |
| p | 0.4 | 0.1 | x |
 如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z:i(i是虚数单位)的共轭复数所对应的点为( )
如图,复平面上的点Z1,Z2,Z3,Z4到原点的距离都相等,若复数z所对应的点为Z1,则复数z:i(i是虚数单位)的共轭复数所对应的点为( ) 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论 已知函数f(x)=lnx-c(x>0)
已知函数f(x)=lnx-c(x>0)