题目内容
11. 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1,有下述结论(1)AC1⊥BC;
(2)$\frac{AD}{D{C}_{1}}$=1;
(3)面FAC1⊥面ACC1A1;
(4)三棱锥D-ACF的体积为$\frac{\sqrt{3}}{3}$.
其中正确的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)连接AB1,则∠B1C1A即为BC和AC1所成的角,由余弦定理,即可判断;
(2)连接AF,C1F,由正三棱柱的定义,即可判断;
(3)连接CD,则CD⊥AC1,且FD⊥AC1,则∠CDF为二面角F-AC1-C的平面角,通过解三角形CDF,即可判断;
(4)由于AD⊥平面CDF,通过VD-ACF=VA-DCF即可求出体积.
解答  解:(1)连接AB1,则∠B1C1A即为BC和AC1所成的角,在三角形AB1C1中,B1C1=2,AB1=2$\sqrt{2}$,
解:(1)连接AB1,则∠B1C1A即为BC和AC1所成的角,在三角形AB1C1中,B1C1=2,AB1=2$\sqrt{2}$,
AC1=2$\sqrt{2}$,cos∠B1C1A=$\frac{8+4-8}{2×2\sqrt{2}×2}$=$\frac{\sqrt{2}}{4}$,
故(1)错;
(2)连接AF,C1F,则易得AF=FC1=$\sqrt{5}$,
又FD⊥AC1,则AD=DC1,故(2)正确;
(3)连接CD,则CD⊥AC1,且FD⊥AC1,
则∠CDF为二面角F-AC1-C的平面角,CD=$\sqrt{2}$,CF=$\sqrt{5}$,DF=$\sqrt{3}$,
即CD2+DF2=CF2,故二面角F-AC1-C的大小为90°,面FAC1⊥面ACC1A1,故(3)正确;
(4)由于CD⊥AC1,且FD⊥AC1,则AD⊥平面CDF,
则VD-ACF=VA-DCF=$\frac{1}{3}$•AD•S△DCF=$\frac{1}{3}×\sqrt{2}×\frac{1}{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{3}}{3}$.故(4)正确.
故选:C.
点评 本题考查正三棱柱的定义和性质,考查线面垂直的判定和性质,空间的二面角,以及棱锥的体积,注意运用转换法,属于中档题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1.“光盘行动”已经发起两年,为了调查人们的节约意识,某班几位同学组成研究性学习小组,从某社区[25,55]岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
(1)求a,b的值,并估计本社区[25,55]岁的人群中“光盘族”人数所占的比例;
(2)从年龄段在[35,45)的“光盘族”中采用分层抽样法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队,求选取的2名领队分别来自[35,40)和[40,45)两个年龄段的概率.
| 组数 | 分组 | 频数 | 频率 | 关盘组占本组的比例 |
| 第一组 | [25,30) | 50 | 0.05 | 30% |
| 第二组 | [30,35) | 100 | 0.1 | 30% |
| 第三组 | [35,40) | 150 | 0.15 | 40% |
| 第四组 | [40,45) | 200 | 0.2 | 50% |
| 第五组 | [45,50) | a | b | 65% |
| 第六组 | [50,55) | 200 | 0.2 | 60% |
(2)从年龄段在[35,45)的“光盘族”中采用分层抽样法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队,求选取的2名领队分别来自[35,40)和[40,45)两个年龄段的概率.
 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1,
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA=AB=AC=1, 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点 A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是( )
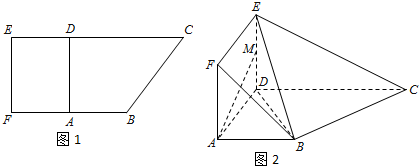
 如图,已知四棱锥P-ABCD中,底面ABCD是平行四边形,BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2,AB=1.
如图,已知四棱锥P-ABCD中,底面ABCD是平行四边形,BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2,AB=1.