题目内容
【题目】一元线性同余方程组问题最早可见于中国南北朝时期（公元
世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：有物不知数，三三数之剩二，五五数之剩三，问物几何？即，一个整数除以三余二，除以五余三，求这个整数.设这个整数为
，当
时，符合条件的共有（ ）
A. 
个B. 
个C. 
个D. 
个
【答案】C
【解析】
由题设a=3m+2=5n+3,m,n
,得3m=5n+1，对m讨论求解即可
由题设a=3m+2=5n+3,m,n,则3m=5n+1
当m=5k,n不存在；
当m=5k+1，n不存在
当m=5k+2,n=3k+1，满足题意
当m=5k+3,n不存在；
当m=5k+4,n不存在；
故2≤a=15k+8≤2019,解
,k∈Z,则k=0,1,2…134,共135个
故选：C
名校课堂系列答案【题目】公历
月
日为我国传统清明节，清明节扫墓我们都要献鲜花，某种鲜花的价格会随着需求量的增加而上升.一个批发市场向某地商店供应这种鲜花，具体价格统计如下表所示
日供应量 |
|
|
|
|
|
|
单位 |
|
|
|
|
|
|
（I）根据上表中的数据进行判断，函数模型
与
哪一个更适合于体现日供应量
与单价
之间的关系；（给出判断即可，不必说明理由）
（II）根据（I）的判断结果以及参考数据，建立关于的回归方程；
（III）该地区有
个商店，其中个商店每日对这种鲜花的需求量在
束以下，
个商店每日对这种鲜花的需求量在束以上，则从这个商店个中任取个进行调查，求恰有
个商店对这种鲜花的需求量在束以上的概率.
参考公式及相关数据：对于一组数据
，
，...，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
.
|
|
|
|
|
|
|
|
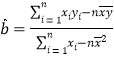【题目】为了研究学生的数学核心素养与抽象能力(指标
)、推理能力(指标
)、建模能力(指标
)的相关性，将它们各自量化为1、2、3三个等级，再用综合指标
的值评定学生的数学核心素养，若
，则数学核心素养为一级；若
，则数学核心素养为二级；若
，则数学核心素养为三级，为了了解某校学生的数学核心素养，调查人员随机访问了某校10名学生，得到如下数据：
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人，求这两人的建模能力指标相同条件下综合指标值也相同的概率；
(2)在这10名学生中任取三人，其中数学核心素养等级是一级的学生人数记为
，求随机变量的分布列及其数学期望.
