题目内容
12.定义在R上的非常值函数f(x)满足y=f(x+1)和y=f(x-1)都是奇函数,则函数y=f(x)一定是( )| A. | 偶函数 | B. | 奇函数 | ||
| C. | 周期函数 | D. | 以上结论都不正确 |
分析 由y=f(x+1)奇函数,即有f(1-x)=-f(1+x),由y=f(x-1)是奇函数,即为f(-x-1)=-f(x-1),将x换成x-1,x+1,再将-x换成x,x换成x+2,结合周期函数的定义,即可得到结论.
解答 解:y=f(x+1)奇函数,
即有f(1-x)=-f(1+x),
将x换成x-1,即有f(2-x)=-f(x),①
y=f(x-1)是奇函数,
即为f(-x-1)=-f(x-1),
将x换成x+1,即有f(-x-2)=-f(x),②
则由①②可得,f(-x-2)=f(2-x),
即有f(x-2)=f(x+2),
将x换成x+2,可得f(x+4)=f(x),
即有函数f(x)是最小正周期为4的函数.
故选:C.
点评 本题考查函数的奇偶性和周期性的定义,考查赋值法的运用,考查一定的推理和分析能力,属于中档题.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
2.已知定义在R上的函数f(x)的导函数为f′(x),对任意x∈R恒有f(x)>f′(x),a=3f(ln2),b=2f(ln3),则有( )
| A. | a>b | B. | a=b | ||
| C. | a<b | D. | a,b大小关系不能判断 |
3.首项为正数的等差数列{an}满足5a6=3a3,则前n项和Sn中最大项为( )
| A. | S9 | B. | S10 | C. | S11 | D. | S12 |
20.车流量被定义为单位时间内通过的十字路口的车辆数,单位为辆/分,上班高峰期某十字路口的车流量有函数F(t)=60+3sin$\frac{t}{3}$(其中0≤t≤20)给出,F(t)的单位是辆/分,t的单位是分,则在下列哪个时间段内车流量是增加的( )
| A. | [15,20] | B. | [10,15] | C. | [5,10] | D. | [0,5] |
7.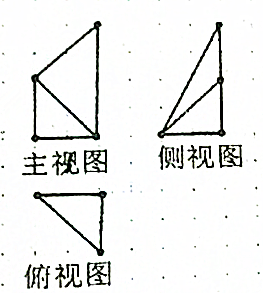 某几何体的三视图如图所示,图中方格的长度为1,则几何体的体积为( )
某几何体的三视图如图所示,图中方格的长度为1,则几何体的体积为( )
 某几何体的三视图如图所示,图中方格的长度为1,则几何体的体积为( )
某几何体的三视图如图所示,图中方格的长度为1,则几何体的体积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
4.定义在R上的函数f(x)满足f(x)+$\sqrt{3}$f($\frac{π}{2}$-x)=sinx,则f($\frac{π}{12}$)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
2.已知α,β∈($\frac{π}{2}$,π),cosα+sinβ>0,则( )
| A. | α+β<π | B. | α+β>$\frac{3π}{2}$ | C. | α+β=$\frac{3π}{2}$ | D. | α+β<$\frac{3π}{2}$ |