题目内容
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目.已知某班第一小组与第二小组各有六位同学选择科目甲或科目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4人均选科目乙的概率;
(2)设
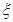 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求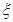 的分布列和数学期望.
的分布列和数学期望.
(1)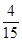 ;(2)分布列详见解析,
;(2)分布列详见解析,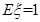 .
.
解析试题分析:(1)选出的4人均选科目乙相当于事件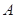 =“从第一小组选出的2人选科目乙”和事件
=“从第一小组选出的2人选科目乙”和事件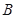 =“从第二小组选出的2人选科目乙”同时发生,由事件
=“从第二小组选出的2人选科目乙”同时发生,由事件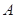 和
和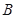 独立,根据独立事件同时发生的概率公式
独立,根据独立事件同时发生的概率公式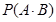
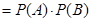 求解;(2)依题意得
求解;(2)依题意得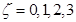 ,分别求其发生的概率,再写出分布列,进而求
,分别求其发生的概率,再写出分布列,进而求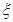 的数学期望 .
的数学期望 .
试题解析:(1)设“从第一小组选出的2人选科目乙”为事件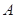 , “从第二小组选出的2人选科目乙”为事件
, “从第二小组选出的2人选科目乙”为事件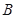 .由于事 件
.由于事 件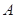 、
、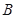 相互独立,
相互独立,
且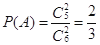 ,
, 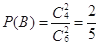 ,所以选出的4人均选科目乙的概率为
,所以选出的4人均选科目乙的概率为 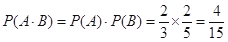
(2)设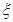 可能的取值为0,1,2,3.得
可能的取值为0,1,2,3.得 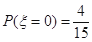 ,
,  ,
,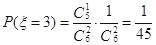 ,
,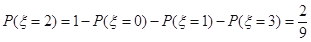
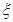 的分布列为
的分布列为
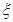 | 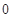 | | 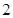 | 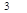 |
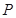 | 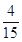 | 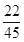 | 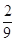 |  |
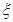 的数学期望
的数学期望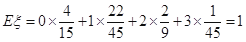
考点:1、组合;2、独立事件同时发生的概率公式;3、分布列和期望.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
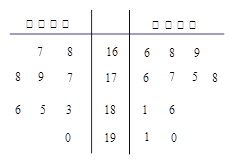
学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.  .
.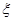 ,试写出
,试写出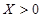 就去打球;若
就去打球;若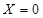 就去唱歌;若
就去唱歌;若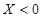 就去下棋.
就去下棋.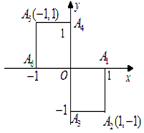
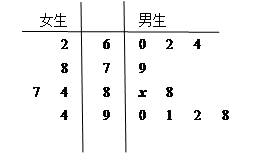
 ,求
,求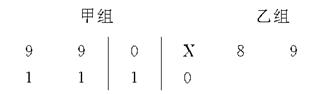
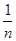 [(x1-
[(x1- )2+(x2-
)2+(x2-