题目内容
(14分)数列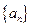 首项
首项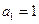 ,前
,前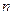 项和
项和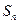 与
与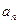 之间满足
之间满足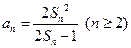
(1)求证:数列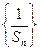 是等差数列
是等差数列
(2)求数列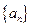 的通项公式
的通项公式
(3)设存在正数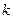 ,使
,使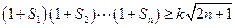 对于一切
对于一切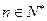 都成立,求
都成立,求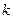 的最大值。
的最大值。
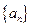 首项
首项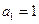 ,前
,前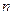 项和
项和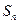 与
与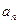 之间满足
之间满足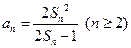
(1)求证:数列
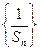 是等差数列
是等差数列 (2)求数列
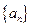 的通项公式
的通项公式(3)设存在正数
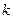 ,使
,使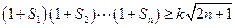 对于一切
对于一切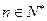 都成立,求
都成立,求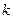 的最大值。
的最大值。解(1)因为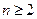 时,
时,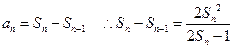 得
得
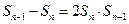 ----------------2分
----------------2分
由题意

又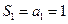
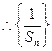 是以
是以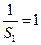 为首项,
为首项,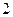 为公差的等差数列 -- 4分
为公差的等差数列 -- 4分
(2)由(1)有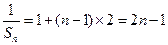
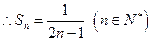 --5分
--5分
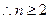 时,
时,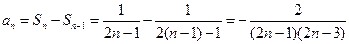 --- 7分
--- 7分
又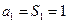
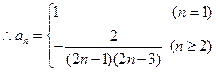 -- (8分)
-- (8分)
(3)设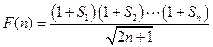 则
则
 -11分
-11分
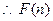 在
在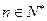 上递增 故使
上递增 故使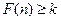 恒成立只需
恒成立只需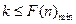
又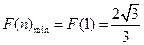 又
又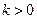
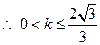 -------13分
-------13分
所以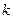 的最大值是
的最大值是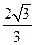 . ---------------(14)
. ---------------(14)
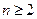 时,
时,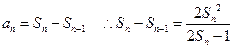 得
得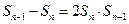 ----------------2分
----------------2分 由题意


又
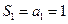
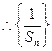 是以
是以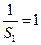 为首项,
为首项,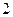 为公差的等差数列 -- 4分
为公差的等差数列 -- 4分(2)由(1)有
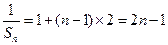
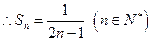 --5分
--5分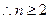 时,
时,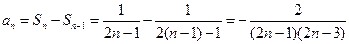 --- 7分
--- 7分又
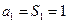
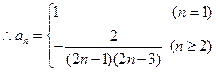 -- (8分)
-- (8分)(3)设
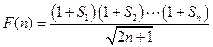 则
则 -11分
-11分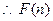 在
在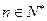 上递增 故使
上递增 故使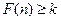 恒成立只需
恒成立只需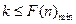
又
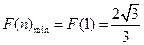 又
又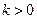
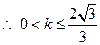 -------13分
-------13分所以
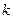 的最大值是
的最大值是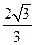 . ---------------(14)
. ---------------(14)略

练习册系列答案
相关题目
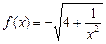 ,点
,点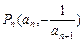 在曲线
在曲线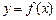 上
上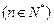 且
且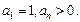 (Ⅰ)求证:数列
(Ⅰ)求证:数列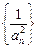 为等差数列,并求数列
为等差数列,并求数列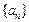 的通项公式;
的通项公式;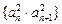 的前n项和为
的前n项和为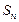 ,若对于任意的
,若对于任意的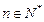 ,存在正整数t,使得
,存在正整数t,使得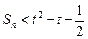 恒成立,求最小正整数t的值
恒成立,求最小正整数t的值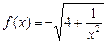 ,点
,点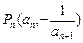 在曲线
在曲线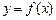 上
上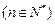 且
且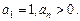 (Ⅰ)求证:数列
(Ⅰ)求证:数列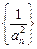 为等差数列,并求数列
为等差数列,并求数列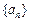 的通项公式;
的通项公式;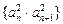 的前n项和为
的前n项和为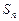 ,若对于任意的
,若对于任意的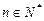 ,存在正整数t,使得
,存在正整数t,使得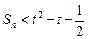 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值. 中,
中,
 ,
, ,则使前
,则使前 项和
项和 成立的最大自然数
成立的最大自然数







 中,已知
中,已知 ,那么
,那么 =( )
=( ) 为等差数列
为等差数列 的前n项的和,
的前n项的和, ,
, ,则
,则 的值为 ( )
的值为 ( ) 中,
中, ,则
,则 的值为
的值为 