题目内容
【题目】已知椭圆C1: ![]() +
+ ![]() =1(a>b>0)过点A(1,
=1(a>b>0)过点A(1, ![]() ),其焦距为2.
),其焦距为2. 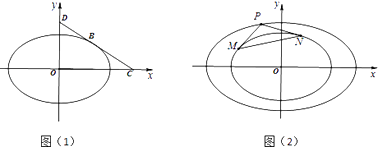
(1)求椭圆C1的方程;
(2)已知椭圆具有如下性质:若椭圆的方程为 ![]() +
+ ![]() =1(a>b>0),则椭圆在其上一点A(x0 , y0)处的切线方程为
=1(a>b>0),则椭圆在其上一点A(x0 , y0)处的切线方程为 ![]() +
+ ![]() =1,试运用该性质解决以下问题:
=1,试运用该性质解决以下问题:
(i)如图(1),点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,求△OCD面积的最小值;
(ii)如图(2),过椭圆C2: ![]() +
+ ![]() =1上任意一点P作C1的两条切线PM和PN,切点分别为M,N.当点P在椭圆C2上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
=1上任意一点P作C1的两条切线PM和PN,切点分别为M,N.当点P在椭圆C2上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
【答案】
(1)解:依题意得:椭圆的焦点为F1(﹣1,0),F2(1,0),由椭圆定义知:2a=|AF1|+|AF2|,
∴ ![]() ,所以椭圆C1的方程为
,所以椭圆C1的方程为 ![]() .
.
(2)解:(ⅰ)设B(x2,y2),则椭圆C1在点B处的切线方程为 ![]()
令x=0, ![]() ,令
,令 ![]() ,所以
,所以 ![]()
又点B在椭圆的第一象限上,所以 ![]() ,
,
∴ ![]()
∴ ![]() ,当且仅当
,当且仅当 ![]()
所以当 ![]() 时,三角形OCD的面积的最小值为
时,三角形OCD的面积的最小值为 ![]()
(ii)设P(m,n),则椭圆C1在点M(x3,y3)处的切线为: ![]()
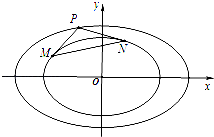
又PM过点P(m,n),所以 ![]() ,同理点N(x4,y4)也满足
,同理点N(x4,y4)也满足 ![]() ,
,
所以M,N都在直线 ![]() 上,
上,
即:直线MN的方程为 ![]()
所以原点O到直线MN的距离 ![]() =
= ![]() ,
,
所以直线MN始终与圆 ![]() 相切.
相切.
【解析】(1)依题意得:椭圆的焦点为F1(﹣1,0),F2(1,0),由椭圆定义知:2a=|AF1|+|AF2|,即可求出a,b,从而可求椭圆C1的方程;(2)(i)确定 ![]() ,再结合基本不等式,即可求△OCD面积的最小值;(ii)先求出直线MN的方程,再求出原点O到直线MN的距离,即可得出结论.
,再结合基本不等式,即可求△OCD面积的最小值;(ii)先求出直线MN的方程,再求出原点O到直线MN的距离,即可得出结论.