题目内容
14.下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y (吨)的4组对应数据:| x | 2 | 4 | 5 | 7 |
| y | 1.5 | t | 4.2 | 5.5 |
分析 根据表中所给的数据,做出横标和纵标的平均数,得到样本中心点,根据由最小二乘法求得回归方程$\stackrel{∧}{y}$=0.7x+0.35,代入样本中心点求出该数据的值.
解答 解:由表中数据得:$\overline{x}$=4.5,$\overline{y}$=$\frac{t+11.2}{4}$,
由于由最小二乘法求得回归方程$\stackrel{∧}{y}$=0.7x+0.35,
将$\overline{x}$=4.5,$\overline{y}$=$\frac{t+11.2}{4}$代入回归直线方程,得m=2.8.
故答案为:2.8
点评 本题考查数据的回归直线方程,利用回归直线方程恒过样本中心点是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.由直线y=0,x=e,y=2x及曲线$y=\frac{2}{x}$所围成的封闭的图形的面积为( )
| A. | 3+2ln2 | B. | 3 | C. | 2e2-3 | D. | e |
5.若动点P在直线l1:x-y-2=0上,动点Q在直线l2:x-y-6=0上,设线段PQ的中点M(a,b),满足a2+b2-4a+4b≤0,则a2+b2的取值范围是( )
| A. | [2$\sqrt{2}$,4] | B. | [2$\sqrt{2}$,2$\sqrt{3}$] | C. | [8,12] | D. | [8,16] |
2.为调查某养老院是否需要志愿服务者提供帮助的情况,用简单随机抽样的方法选取了16名男性和14名女性进行调查,调查发现,男、女中分别有10人和6人需要志愿者提供帮助.
(Ⅰ)根据以上数据完成以下2×2列联表:
(Ⅱ)能否在犯错的概率不超过0.10的前提下推断性别与需要志愿者提供帮助有关?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
(Ⅰ)根据以上数据完成以下2×2列联表:
| 需要 | 不需要 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| K0 | 0.708 | 1.323 | 2.706 | 6.635 |
6.曲线y=ln(x-1)上的点到直线x-y+4=0的最短距离是( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
3.某医院一天派出医生下乡医疗,派出医生人数及其概率如下:
派出的医生至少2人的概率0.74.
| 医生 人数 | 0 | 1 | 2 | 3 | 4 | 5人及以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.2 | 0.2 | 0.04 |
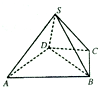 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD. 因为受市场经济的宏观调控,某商品每月的单价和销量均会上下波动,某商家对2015年的1月份到4月份的销售量x百件和利润y万元进行统计分析,得到数据的散点图如图所示:
因为受市场经济的宏观调控,某商品每月的单价和销量均会上下波动,某商家对2015年的1月份到4月份的销售量x百件和利润y万元进行统计分析,得到数据的散点图如图所示: