题目内容
【题目】数列![]() 中,
中,![]() ,当
,当![]() 时,
时,![]() 的前
的前![]() 项和
项和![]() 满足
满足![]()
(1)求![]() 的表达式;
的表达式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)是否存在正整数![]() ,使得
,使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在
(3)存在![]() ,
,![]() 使得
使得![]() 成等比数列.
成等比数列.
【解析】
(1)根据![]() 与
与![]() 的关系
的关系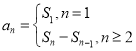 即可找出
即可找出![]() 与
与![]() 的关系,构造等差数列
的关系,构造等差数列![]() , 即可求出
, 即可求出![]() 的表达式;
的表达式;
(2)将![]() 的表达式代入
的表达式代入![]() 求得
求得![]() ,再根据裂项相消法求出
,再根据裂项相消法求出![]() ,化简可得
,化简可得![]() ,由数列极限的运算法则即可求出;
,由数列极限的运算法则即可求出;
(3)假设存在,根据![]() 成等比数列得到
成等比数列得到![]() ,看是否能解出符合的解即可判断.
,看是否能解出符合的解即可判断.
(1)当![]() 时,
时,![]() ,代入
,代入![]() ,化简可得
,化简可得![]() ,
,
![]() ,所以数列
,所以数列![]() 为等差数列,即有
为等差数列,即有![]() ,
,
故![]() .
.
(2)由(1)知,![]() ,所以
,所以![]() ,
,
![]() ,
,
故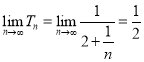 .
.
(3)假设存在,根据![]() 成等比数列得到
成等比数列得到![]() ,即
,即![]() ,
,
化简得,![]() ,所以
,所以![]() ,又因为
,又因为![]() ,解得
,解得
![]() ,而
,而![]() ,
,![]() ,故
,故![]() ,代入
,代入![]() ,解得
,解得![]() .
.
综上,存在![]() ,
,![]() 使得
使得![]() 成等比数列.
成等比数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目