题目内容
3.从5双不同号的鞋子中任取4只,求(1)恰有2只同号的概率;
(2)至少有2只同号的概率.
分析 从10只鞋子中任取4只,共有C104=210不同的取法;
(1)恰好有两只同号不同取法有C51C42C21C21种取法,由此能求出恰有2只同号的概率;
(2)取出的四只鞋都不同号的方法有 C54×2×2×2×2=80,则至少有2只同号的取法种数是210-80=130,由此能求出至少有2只同号的概率.
解答 解:(1)从10只鞋子中任取4只,共有C104=210不同的取法,
恰有2只同号的取法是先从5双不同号的鞋子中任取一种号码的一双鞋子,有C51种取法,
再从剩余4双不同号的鞋子中任取两种号码的鞋子各一只,有C42C21C21种取法,
∴恰好有两只同号的不同取法有C51C42C21C21=120种取法,
故恰有2只同号的概率为$\frac{120}{210}$=$\frac{4}{7}$;
(2)取出的四只鞋都不同号的方法有 C54×2×2×2×2=80,
则至少有2只同号的取法种数是210-80=130,
故至少有2只同号的概率为$\frac{130}{210}$=$\frac{13}{21}$.
点评 本题考查等可能事件的概率,考查组合知识的运用.解题时要认真审题,注意排列组合的合理运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知sin(α+π)=-$\frac{1}{2}$,则$\frac{1}{cos(-α+7π)}$的值是( )
| A. | -2 | B. | -$\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | ±$\frac{2\sqrt{3}}{3}$ |
18.把函数f(x)=sin(ωx+$\frac{π}{3}$)(ω>0)的图象向右平移$\frac{π}{6}$个单位后,得到函数g(x)的图象,若g(x)为偶函数,则ω的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.观察分析下表中的数据:
猜想一般凸多面体中,面数、顶点数、棱数:F、V、E所满足的等式是F+V=E+2.
| 多面体 | 面数(F) | 顶点数(V) | 棱数(E) |
| 三棱锥 | 5 | 6 | 9 |
| 五棱锥 | 6 | 6 | 10 |
| 立方体] | 6 | 8 | 12 |
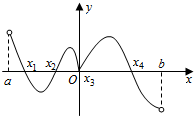 函数f(x)的定义域为(a,b),其导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在区间(a,b)内极小值点的个数是( )
函数f(x)的定义域为(a,b),其导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在区间(a,b)内极小值点的个数是( )