题目内容
【题目】已知函数![]()
(1)当![]() 时,求函数的单调区间;
时,求函数的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上的最小值记为
上的最小值记为![]() ,请写出
,请写出![]() 的函数表达式。
的函数表达式。
【答案】(1)单调增区间![]() ,单调减区间
,单调减区间![]()
(2)
【解析】
(1)求出函数的导数,由![]() ,可得
,可得![]() ;由
;由![]() 可得
可得![]() ,从而得单调区间;
,从而得单调区间;
(2)求出函数的导数,通过讨论a的范围,确定函数的单调区间,从而求出区间上的最小值即可.
(1)∵![]() ,
,
∴![]()
当a=1时,![]() ,
,
由![]() ,可得
,可得![]() ;由
;由![]() 可得
可得![]() .
.
所以单调增区间![]() ,单调减区间
,单调减区间![]() .
.
(2)![]() ,
,
∵a>0,x>0,由f′(x)>0得x>2a,由f′(x)<0得0<x<2a,
∴f(x)在(0,2a]上为减函数,在(2a,+∞)上为增函数.
①当0<2a≤1即0<a![]() 时,f(x)在[1,2]上为增函数,
时,f(x)在[1,2]上为增函数,
∴g(a)=f(1)=2a2+1.
②当1<2a<2即![]() a
a![]() 时,f(x)在[1,2a]上为减函数,在(2a,2]上为增函数,
时,f(x)在[1,2a]上为减函数,在(2a,2]上为增函数,
∴g(a)=f(2a)=﹣aln(2a)+3a
③当2a≥2即a![]() 时,f(x)在[1,2]上为减函数,
时,f(x)在[1,2]上为减函数,
∴![]()
综上所述,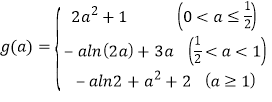 .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案【题目】随着我国互联网信息技术的发展,网络购物已经成为许多人消费的一种重要方式,某市为了了解本市市民的网络购物情况,特委托一家网络公示进行了网络问卷调查,并从参与调查的10000名网民中随机抽取了200人进行抽样分析,得到了下表所示数据:
经常进行网络购物 | 偶尔或从不进行网络购物 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)依据上述数据,能否在犯错误的概率不超过![]() 的前提下认为该市市民进行网络购物的情况与性别有关?
的前提下认为该市市民进行网络购物的情况与性别有关?
(2)现从所抽取的女性网民中利用分层抽样的方法再抽取![]() 人,从这
人,从这![]() 人中随机选出
人中随机选出![]() 人赠送网络优惠券,求出选出的
人赠送网络优惠券,求出选出的![]() 人中至少有两人是经常进行网络购物的概率;
人中至少有两人是经常进行网络购物的概率;
(3)将频率视为概率,从该市所有的参与调查的网民中随机抽取![]() 人赠送礼物,记经常进行网络购物的人数为
人赠送礼物,记经常进行网络购物的人数为![]() ,求
,求![]() 的期望和方差.
的期望和方差.
附:![]() ,其中
,其中![]()

