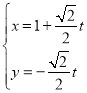题目内容
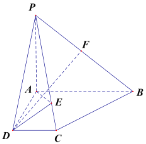
【题目】已知点![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 是该椭圆上一点,若当
是该椭圆上一点,若当![]() 时,
时,![]() 面积达到最大,最大值为
面积达到最大,最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,是否存在过左焦点
为坐标原点,是否存在过左焦点![]() 的直线
的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,使得
两点,使得![]() 的面积为
的面积为![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 或
或![]() .
.
【解析】
(1)利用![]() 面积最大值为
面积最大值为![]() ,可得
,可得![]() ,结合
,结合![]() 及
及![]() 的关系可得椭圆
的关系可得椭圆![]() 的标准方程;
的标准方程;
(2)设出直线方程,利用韦达定理及面积公式,建立方程,可得直线方程.
(1)由题可知当点![]() 在短轴端点时,
在短轴端点时,![]() 面积最大值为
面积最大值为![]() ①,
①,
此时![]() ,
,![]() ,所以
,所以![]() ②,
②,
又知![]() ③,由上述3个式子解得
③,由上述3个式子解得![]() ,
,![]() ,
,![]() .
.
所以椭圆C的标准方程为![]() .
.
(2)存在,由(1)![]() ,由题意可知直线
,由题意可知直线![]() 与
与![]() 轴不重合,所以设
轴不重合,所以设![]() :
:![]() ,
,
与椭圆方程联立得![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
![]() ,解得
,解得![]() ,
,
即直线![]() 方程为
方程为![]() 或
或![]() .
.

【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】第十三届全国人大第二次会议于2019年3月5日在北京开幕.为广泛了解民意,某人大代表利用网站进行民意调查.数据调查显示,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组
.现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
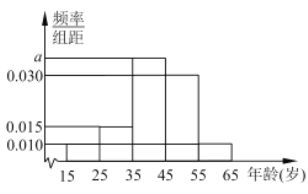
(1)求![]() ;
;
(2)现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人,并再从这5人中随机抽取2人接受现场访谈,求这两人恰好属于不同组别的概率;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的中老年人有10人,问是否有![]() 的把握认为是否关注民生与年龄有关?
的把握认为是否关注民生与年龄有关?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
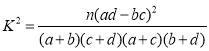 ,
,![]() .
.