题目内容
已知曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差是1。
(Ⅰ)求曲线C的方程;
(Ⅱ)过点K(-1,0)的直线l与C相交于A、B两点,点A关于x轴的对称点为D。证明:点F在直线BD上;
(Ⅰ)求曲线C的方程;
(Ⅱ)过点K(-1,0)的直线l与C相交于A、B两点,点A关于x轴的对称点为D。证明:点F在直线BD上;
解:(Ⅰ)根据题意知,C上每一点到点F(1,0)的距离等于它到直线 的距离。
的距离。
所以,曲线C上每一点在开口向右的抛物线上, ……2分
其中 ,所以抛物线方程为
,所以抛物线方程为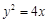 。
。
又因为曲线C在y轴的右边,所以,曲线C的方程为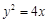 (
( )。 ……2分
)。 ……2分
(Ⅱ)设A(x1,y1),B(x2,y2),∴D(x1,-y1),l的方程为 (m≠0)。
(m≠0)。
将 代人
代人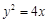 ,整理得
,整理得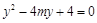 ,
,
∴从而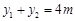 ,
, 。 ……2分
。 ……2分
直线BD的方程为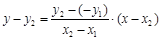 ,
,
即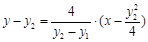 , ……2分
, ……2分
令y=0,得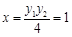 ,所以点F(1,0)在直线BD上。▋ ……2分
,所以点F(1,0)在直线BD上。▋ ……2分
 的距离。
的距离。所以,曲线C上每一点在开口向右的抛物线上, ……2分
其中
 ,所以抛物线方程为
,所以抛物线方程为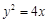 。
。又因为曲线C在y轴的右边,所以,曲线C的方程为
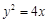 (
( )。 ……2分
)。 ……2分(Ⅱ)设A(x1,y1),B(x2,y2),∴D(x1,-y1),l的方程为
 (m≠0)。
(m≠0)。将
 代人
代人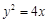 ,整理得
,整理得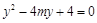 ,
,∴从而
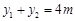 ,
, 。 ……2分
。 ……2分直线BD的方程为
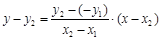 ,
,即
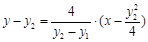 , ……2分
, ……2分令y=0,得
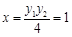 ,所以点F(1,0)在直线BD上。▋ ……2分
,所以点F(1,0)在直线BD上。▋ ……2分略

练习册系列答案
相关题目
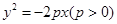 上,则它的边长为( )
上,则它的边长为( )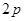


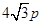
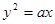 的准线是直线
的准线是直线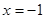 ,那么它的焦点坐标是 ( )
,那么它的焦点坐标是 ( )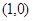



 的焦点坐标为: .
的焦点坐标为: .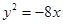 上一点,设P到此抛物线准线的距离是
上一点,设P到此抛物线准线的距离是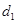 ,到直线
,到直线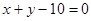 的距离是
的距离是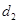 ,则
,则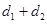 的最小值是
的最小值是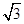
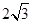
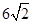
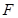 是抛物线
是抛物线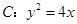 的焦点,过
的焦点,过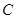 于
于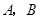 两点.则
两点.则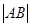 的值等于 .
的值等于 .  若x≥0,则动点
若x≥0,则动点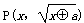 的轨迹是
的轨迹是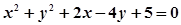 的圆心.
的圆心.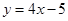 的距离最短,并求距离的最小值.
的距离最短,并求距离的最小值.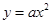 的焦点坐标为
的焦点坐标为 ,则
,则 的值为
的值为